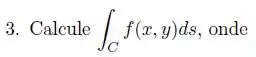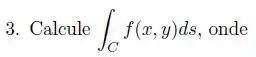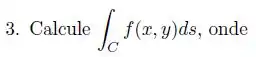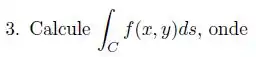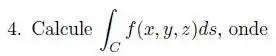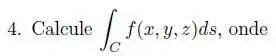Listas GMA de Cálculo IIIA da UFF - Lista 3

1. Apresente uma parametrização diferenciável para as seguintes curvas planas:

1. Apresente uma parametrização diferenciável para as seguintes curvas planas:

1. Apresente uma parametrização diferenciável para as seguintes curvas planas:

1. Apresente uma parametrização diferenciável para as seguintes curvas planas:

1. Apresente uma parametrização diferenciável para as seguintes curvas planas:

1. Apresente uma parametrização diferenciável para as seguintes curvas planas:

1. Apresente uma parametrização diferenciável para as seguintes curvas planas:

1. Apresente uma parametrização diferenciável para as seguintes curvas planas:

1. Apresente uma parametrização diferenciável para as seguintes curvas planas:

1. Apresente uma parametrização diferenciável para a curva em , interseção das superfícies dadas por:

1. , e

1. Apresente uma parametrização diferenciável para a curva em , interseção das superfícies dadas por:

1. e , , situada no primeiro octante.

1. Apresente uma parametrização diferenciável para a curva em , interseção das superfícies dadas por:

1. e .

1. Apresente uma parametrização diferenciável para a curva em , interseção das superfícies dadas por:

1. situada no primeiro octante.

1. Apresente uma parametrização diferenciável para a curva em , interseção das superfícies dadas por:

Calcule

Onde e é formada pelo arco da parábola de a seguido pelo segmento de reta vertical de a .

Calcule

Onde e é a curva interseção das superfícies , com e .

Calcule

Onde e é a curva interseção das superfícies e situada no primeiro octante.

Calcule

Onde e é a interseção do cilindro parabólico com a parte do plano , tal que .

Seja a curva interseção da semiesfera , com o plano . Determine o valor de , se

Sabendo que

Onde é a elipse

Calcule a área da região limitada pela elipse.

Um pedaço de arame tem a forma da curva interseção da esfera como plano . Calcule a massa do arame se a densidade é dada por .

Achar a massa da curva dada por , , , , se a densidade em cada ponto é inversamente proporcional ao quadrado da distância do ponto à origem.

1. Calcule a primeira coordenada do centro de massa de um fio homogêneo que está ao longo de uma curva

Um arame tem a força de uma curva obtida como interseção da semiesfera , , com o plano . Sabendo que a densidade em cada ponto é dada por , mostre que o momento de inércia em relação ao eixo é igual a , onde é a massa do arame.

1. Calcule a massa da elipse , situada no primeiro quadrante, se a densidade em cada ponto é igual ao produto das coordenadas do ponto.

Calcule a área de uma lado da superfície cuja base é a circunferência , no plano , e a altura em cada ponto é .

1. Deseja-se construir uma peça de zinco que tem a forma da superfície do cilindro , compreendida entre os planos e , . Se o metro quadrado do zinco custa reais, calcule o preço total da peça.

Um pintor deseja pintar os dois lados de uma cerca cuja base é uma curva no plano dada por , para e . A altura em cada ponto é dada por . Se o pintor cobra reais por , quanto ele receberá?

Seja dado um arame semicircular homogêneo de raio .

1. Mostre que o centro de massa está situado no eixo de simetria a uma distância de do centro
2. Mostre que o momento de inércia em relação ao diâmetro que passa pelos extremos do arame é , sendo a massa do arame.

1. Um arame fino é entortado no formato da curva das superfícies e , situado no primeiro octante e que liga o ponto ao ponto . Calcule a massa do arame, sendo a densidade em cada ponto proporcional ao quadrado da distância do ponto ao plano .

Um arame fino tem a forma da curva de interseção das superfícies e , . Determine a massa do arame, se a densidade em qualquer ponto é igual ao quadrado da distância do ponto ao plano .

1. Calcule o momento de inércia de um fio retilíneo homogêneo de comprimento , em torno de um eixo perpendicular ao fio e passando por uma das extremidades do fio, em função de sua massa.

Um fio delgado tem a forma de reta que une os pontos e . Determine o momento de inércia em relação à reta , supondo que a densidade no ponto é proporcional à distância do ponto ao eixo .