- Apresente uma parametrização diferenciável para a curva em , interseção das superfícies dadas por:
-
e , , situada no primeiro octante.
Passo 1
Bem, será de grande ajuda se você sempre começar parametrizações assim, desenhando essa curva no espaço.
Mas calma, pois basta colocar essas superfícies juntas no que você verá a curva na intercessão delas! Veja:
é uma esfera de raio e é um cilindro de raio ...
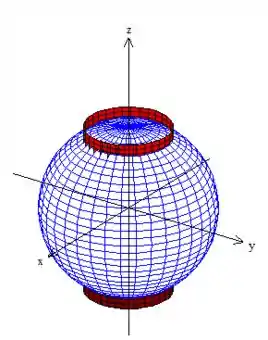
E eis a curva como intercessão delas e no primeiro octante!
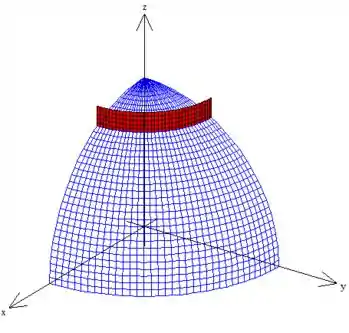
Passo 2
Como estamos em cima de um cilindro, podemos pensar na parametrização cilíndrica (semelhante às mudanças para coordenadas cilindricas ;)
Como o raio do cilindro é ...
Quanto ao , bem repare que ele é dado pela intercessão do cilindro com a esfera. Fazer isso em matemática é resolver o sistema com as duas equações:
Como estamos trabalhando no primeiro octante...
Logo:
Passo 3
Agora se lembre: nunca devemos terminar uma parametrização sem encontrar onde esse parâmetro está variando, ok?
Nesse caso, como pode ser notado no desenho, só queremos o pedaço de curva que está acima no primeiro octante, então com dando um quarto de volta: