- Apresente uma parametrização diferenciável para as seguintes curvas planas:
-
Passo 1
Pow! É sempre muito recomendado que se desenhe a curva antes de parametriza-la.
Bem, essa curva nos representa a parte do lado de uma elipse centrada na origem (a parte de lado, pois )
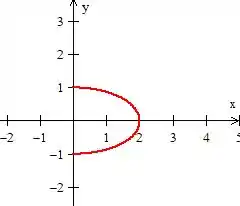
Ahhh! Não se preocupe em desenhar essa elipse com perfeição. Isso não importa muito aqui ;)
Passo 2
Pow, elipses assim, sempre podemos passa-la para sua fórmula geral:
onde a parametrização sempre será:
No nosso caso...
Assim, uma parametrização é:
dá uma meia volta partindo de baixo ( abaixo) então...
Passo 3
Agora basta verificar se ela é diferenciável calculando sua derivada:
Repare que essa derivada aí funciona para qualquer ponto. Então, sim, ela é diferenciável !
Resposta
Exercícios de Livros Relacionados
Para cada um dos seguintes pares de equações paramétricas, esboce a curva e determine a sua equação cartesiana.
Para cada um dos seguintes pares de equações paramétricas, esboce a curva e determine a sua equação cartesiana.
Esboçar as curvas seguintes, representando o sentido positivo de percurso. Obter uma parametrização da curva dada, orientada no sentido contrário.d) r → t = 2 cos 3 t ,2 s e n 3 t , t ∈ 0 , π 2
Esboçar as curvas seguintes, representando o sentido positivo de percurso. Obter uma parametrização da curva dada, orientada no sentido contrário.b) r → t = t ,t + 2 ,4 - 2 t , t ∈ 0 ,1
Esboçar as curvas seguintes, representando o sentido positivo de percurso. Obter uma parametrização da curva dada, orientada no sentido contrário.a) r → t = 2 + 3 cos t ,1 + 4 s e n t , t ∈ 0 ,2 π