- Apresente uma parametrização diferenciável para a curva em , interseção das superfícies dadas por:
-
, e
Passo 1
Bem, será de grande ajuda se você sempre começar parametrizações assim, desenhando essa curva no espaço.
Mas calma, pois basta colocar essas superfícies juntas no que você verá a curva na intercessão delas! Veja:
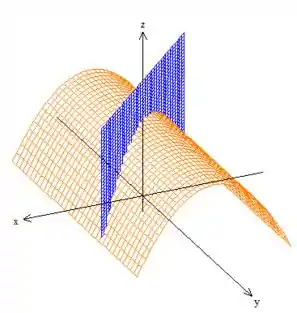
Observe que nesse caso, a curva está em cima desse cilindro parabólico de equação explícita . Logo podemos pensar em uma parametrização... explícita...
Passo 2
Nesse tipo de parametrização, troquemos o
como a curva está em cima do plano ...
também, saca? Enquanto o ...
Logo, a parametrização fica...
Passo 3
Agora se lembre: nunca devemos terminar uma parametrização sem encontrar onde esse parâmetro está variando, ok?
Nesse caso, como pode ser notado no desenho, só queremos o pedaço de curva que está acima de . Como ...
portanto, podemos falar que
Resposta
Exercícios de Livros Relacionados
Como se calcula a área de uma superfície parametrizada no espa-ço? E de uma superfície implicitamente definida F(x, y, z) = 0?E da superfície que é o gráfico de z = ƒ(x, y)? Dê exemplos
Calcule 1C F ∙ T ds para o campo vetorial F = x2i – yj ao longoda curva x = y2 de (4, 2) a (1, –1).
Calcule int_C x y d x + ( x + y ) d y ao longo da curva y = x^2 de ( - 1,1 ) a ( 2,4 )
O que são integrais de linha? Como elas são calculadas? Dêexemplos
Calcule as integrais nos Exercícios 9 e 10.10. ∫ y 2d x + x 2d x C é a circunferência x 2 + y 2 = 4 .