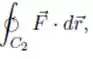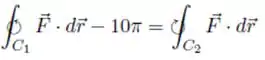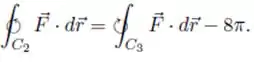Listas GMA de Cálculo IIIA da UFF - Lista 4

Seja a interseção do cilindro com o semiplano , , percorrida de modo que sua projeção no plano tenha sentido anti-horário e seja . Calcule a integral

O campo de forças atua sobre uma partícula transladando-a ao longo da curva interseção das superfícies e , orientada de modo que sua projeção no plano seja percorrida uma vez, no sentido horário. Calcule o trabalho realizado por

1. Calcule o trabalho realizado pela força para deslocar uma partícula ao longo da curva interseção das superfícies e , orientada do ponto a .

1. Achar o trabalho de uma força variável, dirigida para a origem das coordenadas, cuja grandeza é proporcional ao afastamento do ponto em relação à origem das coordenas, se o ponto de aplicação desta força descreve, no sentido anti-horário, a parte da elipse no primeiro quadrante.

Um campo de forças bidimensional define-se por

1. Prove que o trabalho realizado por esta força ao deslocar uma partícula ao longo da curva , depende unicamente de , , e .
2. Determine o trabalho realizado quando , , e

Uma partícula de peso desce de a ao longo da parábola . Agem sobre a partícula a força de gravidade e também uma força horizontal dirigida para a direita, de módulo igual à coordenada do ponto. Determine o trabalho realizado por essas duas forças.

Seja uma função diferenciável e uma primitiva de , tal que , . Calcule

Onde está situada no primeiro octante, e é a interseção das superfícies e , percorrida no sentido anti-horário quando vista de cima.

Verifique o Teorema de Green, calculando as duas integrais do enunciado, para

Onde é a região interior à elipse .

Se é a região interior a elipse e exterior à circunferência , calcule a integral de linha

Onde está positivamente orientada.

16) Calcule as seguintes integrais:

f)

onde é a fronteira da região entre as circunferências e , orientada positivamente.

18) Calcule o trabalho realizado pelo campo de forças

ao mover uma partícula ao longo da trajetória dada por .

Considere o campo vetorial dado por , onde . Calcule , onde é a elipse , percorrida no sentido anti-horário.

20) Seja de classe , tal que . Considere o campo . Calcule onde é a curva formada por e .

21) Seja um campo vetorial de classe , em tal que , para todo . Sabendo que , onde , calcule

Onde .

22) Considere um campo definido em tal que em . Suponha que , e , . Calcule

23) Calcule onde

e é a curva fechada formada pelas curvas , e , , percorrida no sentido anti-horário.

24) Calcule

Onde é a curva , , orientada de à

25) Seja

Calcule a integral de linha do campo ao longo de e , orientadas no sentido anti-horário, onde

Seja uma curva simétrica em relação ao eixo , que vai de a , como mostrada na figura abaixo. Sabendo-se que a área da região delimitada por e o eixo vale 16, calcule o trabalho realizado pela força

27) Calcule

Onde

e é a curva , , percorrida de a .

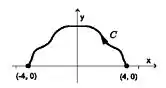
28) Seja de classe em , tal que , sejam , e . Calcule

Sabendo que

e

29) Calcule

onde é o arco da parábola de a .

Seja

1. é conservativo? Por quê?
2. Calcule ,
3. Calcule , , orientada no sentido anti-horário

31) Calcule, onde

e é dada por...

1. .
2. .

32) Seja qualquer curva unindo qualquer ponto na circunferência a qualquer ponto na circunferência , . Seja . Mostre que tem sempre o valor .

33) Verifique que a seguinte integral independe do caminho e calcule o seu valor:

Encontre todos os valores possíveis de

Onde é uma curva fechada qualquer que não passa pela origem.

35) Considere a curva parametrizada por , com Calcule onde

36) Calcule

Onde

e é a semicircunferência , com , orientada de a .

Calcule , onde e é a curva parametrizada por

Verificar que a integral

Independe do caminho e calculo o seu valor.

1. Calcule de a ao longo

1. do eixo

Calcule

Onde e é a interseção das superfícies e , percorrida no senti anti-horário quando vista da origem.

1. Calcule , ao longo dos seguintes caminhos fechados, orientados no sentido anti-horário.

1. circunferência de centro na origem e raio .

1. Calcule de a ao longo

1. de :

1. Calcule , do ponto ao ponto , ao longo dos seguintes cainhos:

1. Segmento de reta

1. Calcule , ao longo dos seguintes caminhos fechados, orientados no sentido anti-horário.

1. Elipse .

1. Calcule de a , ao longo

1. do arco de circunferência , orientada no sentido anti-horário.

1. Calcule de a , ao longo

1. do arco da parábola .

1. Calcule de a , ao longo

1. do segmento de reta.

1. Calcule , do ponto ao ponto , ao longo dos seguintes cainhos:

1. interseção das superfícies e .

1. Calcule , ao longo dos seguintes caminhos fechados, orientados no sentido anti-horário.

1. Triângulo de vértices e .

1. Calcule

Onde:

1. e é a interseção das superfícies e , com e , percorrida uma vez do ponto ao .

1. Calcule de a ao longo

1. da poligonal de vértices: e

1. Calcule

Onde:

1. e é a interseção das superfícies e , orientada de modo que sua projeção no plano se percorrida uma vez no sentido horário.

16) Calcule as seguintes integrais:

b)

onde é formada por , e .

16) Calcule as seguintes integrais:

d)

onde é a fronteira da região limitada por e .

15) Calcule as integrais de linha diretamente e também e também pelo Teorema de Green:

a)

onde é a circunferência unitária , , com .

17) Calcule as seguintes integrais:

b)

Onde é a curva , , percorrida de a .

17) Calcule as seguintes integrais:

d)

Onde é o arco de parábola , orientado de a .

16) Calcule as seguintes integrais:

e)

onde é a fronteira da região limitada pelas curvas e .

16) Calcule as seguintes integrais:

a)

onde é a circunferência .

16) Calcule as seguintes integrais:

c)

onde é a fronteira da região limitada por , e , com .

15) Calcule as integrais de linha diretamente e também e também pelo Teorema de Green:

b)

onde é o caminho fechado formado por , e , orientado positivamente.

17) Calcule as seguintes integrais:

a)

Onde é formada por e , , que vai do ponto ao ponto .

17) Calcule as seguintes integrais:

c)

Onde é a poligonal aberta que une os pontos , e , nesta ordem.