Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Caso Escalar R²

Ver Teoria
Exercício 181234567891011121314151617192021222324252627282930313233343536373839404142434445464748495051525354555657585960

Enunciado

  1. Deseja-se construir uma peça de zinco que tem a forma da superfície do cilindro x 2 + y 2 = 4 , compreendida entre os planos z = 0 e x + y + z = 2 , z ≥ 0 . Se o metro quadrado do zinco custa M reais, calcule o preço total da peça.

Passo 1

Então, precisamos encontrar a área dessa superfície que está em cima de um cilindro x 2 + y 2 = 4

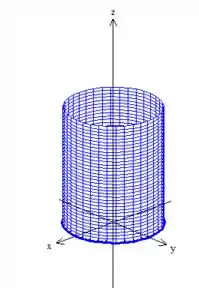
certo? Mas como podemos fazer isso?

Podemos utilizar uma integral de linha!!!

Pensa comigo! Se pegássemos aquela “linha azul” da base do cilindro e multiplicássemos pela altura, teríamos a área dessa casca, correto?

Então... Se considerarmos essa linha de base como a curva C e a altura for dada por uma função h ( x ,   y ) , podemos calcular sua área como sendo:

Á r e a = ∫ C   h x ,   y d S

Pense no d S com um pedacinho da curva C , vezes a altura h , encontrasse a área de uma faixa. A integral de linha, soma todas essas áreas dando a área total da casca que buscamos, saca?:)

Surgem aqui então, dois problemas:

  1. Quem é a altura h ( x ,   y ) ?
  2. Quem é a curva de base C ?

Passo 2

Pra responder a primeira pergunta, vamos desenhar rapidinho a o esboço da nossa peça que é o cilindro de cima,

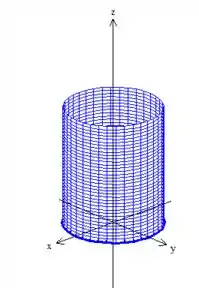
delimitada pelo plano x + y + z = 2 :

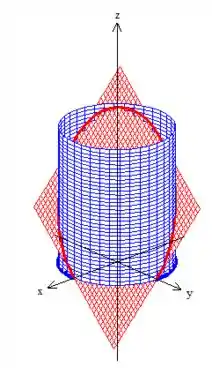
Eis que a peça é...

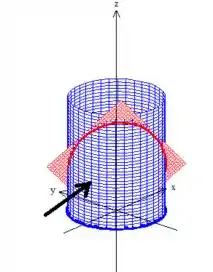
essa apontada pela flecha!

Com esse esboço, podemos falar que a altura h ( x ,   y ) que procuramos está sendo delimitada pelo plano x + y + z = 2 . Basta que isolemos z em função de x e y e...

h x ,   y = z = 2 - x - y

temos a nossa altura!

Passo 3

Quanto à segunda pergunta, a respeito da curva C , bem note que a Curva de base do cilindro é a própria intercessão do cilindro com o plano z = 0 , formando essa circunferência aqui:

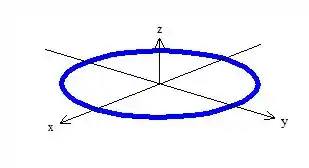
Melhor visualizando, essa daqui oh:

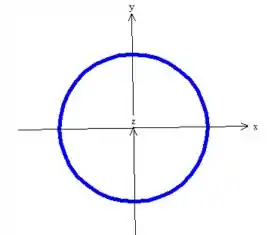
Sua equação... É a própria equação do cilindro: x 2 + y 2 = 4 , percebeu?

Passo 4

Respondida as duas perguntas, podemos passar para a resolução da integral de linha propriamente dito e não fazemos nada se não tivermos a nossa “linha” parametrizada.

Como estamos dentro de uma circunferência, podemos trabalhar com a parametrização prima das coordenadas polares:

x = R a i o   d a   c i r c u n f e r ê n c i a ⋅ cos ⁡ θ

y = R a i o   d a   c i r c u n f e r ê n c i a ⋅ sin ⁡ θ

Como o raio no caso é 2 , pois x 2 + y 2 = 2 2 ...

x = 2 cos ⁡ θ

y = 2 sin ⁡ θ

Então, a parametrização mais organizada é

r θ = 2 cos ⁡ θ ,   2 sin ⁡ θ

Como podemos perceber na imagem da curva...

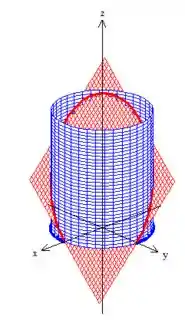
ou vista de cima pra baixo na projeção no plano x y ...

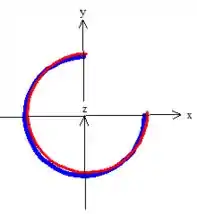
θ está variando de 90 ° até o 360 ° :

π 2 ≤ θ ≤ 2 π

Passo 5

Sendo assim, a nossa próxima função aqui é justamente mudar a função h x ,   y = 2 - x - y para os termos dessa parametrização (basta trocar esse x , y e aí)

h x ,   y = 2 - x - y   →

h r θ = 2 - 2 cos ⁡ θ - 2 sin ⁡ θ   →

h r θ = 2 1 - cos ⁡ θ - sin ⁡ θ

Passo 6

Devemos agora encontrar o termo d s fazendo

d s = r ' θ d θ

derivando a curva portanto...

r θ = 2 cos ⁡ θ ,   2 sin ⁡ θ →       r ' θ = - 2 sin ⁡ θ ,   2 cos ⁡ θ

extraindo o módulo desse vetor derivada...

r ' θ = - 2 sin ⁡ θ 2 + 2 cos ⁡ θ 2 =

r ' ( θ ) = 4 sin 2 ⁡ θ + 4 cos 2 ⁡ θ =

r ' ( θ ) = 4 = 2

d s = 2   d θ

Passo 7

Podemos então, finalmente regressar à integral de linha que precisamos resolver e substituir tudo:

Á r e a = ∫ C   h x ,   y d S

Trocando C pela variação do parâmetro...

Á r e a = ∫ π 2 2 π 2 1 - cos ⁡ θ - sin ⁡ θ   ⋅ 2 d θ

Agora é só integrar!

∫ π 2 2 π 2 1 - cos ⁡ θ - sin ⁡ θ   ⋅ 2 d θ =

4 ∫ π 2 2 π 1 - cos ⁡ θ - sin ⁡ θ   d θ =

4 θ - sin ⁡ θ + cos ⁡ θ π 2 2 π =

4 2 π - sin ⁡ 2 π + cos ⁡ 2 π - π 2 - sin ⁡ π 2 + cos ⁡ π 2 =

4 2 π - 0 + 1 - π 2 - 1 + 0 =

4 3 π 2 + 2 =

6 π + 8

Passo 8

A área é 6 π + 8 , se o preço por metro quadrado é M , então preço total da peça é...

6 π + 8 M

Resposta

6 π + 8 M

Exercícios de Livros Relacionados

Calcule a integral de linha, onde C é a curva dada. ∫ C x + 2 y d x + x 2 d y C consiste nos segmentos de reta de ( 0,0 ) a ( 2,1 ) e de ( 2,1 ) a ( 3,0 ) .
Calcule o valor da integral de linha, onde C é a metade é a metade do círculo x 2 + y 2 = 16
Calcule a integral de linha, onde C é a curva dada.int_C x y^3 d s , C : x = 4 s e n t , y = 4 cos t , z = 3 t , 0 = t = (pi)/(2)
Determine o valor exato de ∫ C x 3 y 5d s , onde C é a parte da astróide x = c o s 3 t , y = s e n 3 t no primeiro quadrante.
Calcule a integral de linha, onde C é a curva dada.int_C x y^4 d s , C é a m e t a d e d i r e i t a d o c í r c u l o x^2 + y^2 = 16 é í