Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Parametrizações Clássicas

Ver Teoria
Exercício 8123456791011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768697071727374757677787980818283848586878889

Enunciado

  1. Apresente uma parametrização diferenciável para as seguintes curvas planas:
  1. C : x 2 + y 2 = 16 ,         x ≥ 2

Passo 1

Pow! É sempre muito recomendado que se desenhe a curva antes de parametriza-la.

Bem, nesse caso estamos trabalhando com uma circunferência de raio 4 : x 2 + y 2 = 16 ,

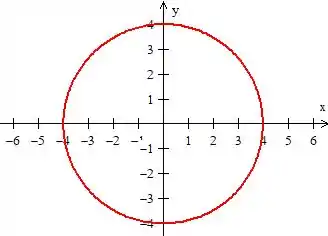
porém, só queremos a parte onde o x ≥ 2

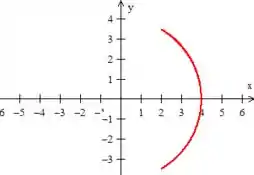
Passo 2

Pow! Circunferências sempre podemos parametrizar semelhante as coordenadas polares:

x = r cos ⁡ θ

y = r sin ⁡ θ

Mas cuidado! Como estamos parametizando curvas, só temos um parâmetro e não dois, então esse r desparece, afinal de contas o raio dessa circunferência é 4 :

x = 4 cos ⁡ θ

y = 4 sin ⁡ θ

Assim, uma parametrização é:

r → t = 4 cos ⁡ θ ,   4 sin ⁡ θ

Passo 3

Precisamos encontrar, como em qualquer parametrização, a variação de θ agora. Bem, repare que θ atinge o seu máximo na bordinha da curva, onde x = 2 , logo...

x = 4 cos ⁡ θ       →         2 = 4 cos ⁡ θ       →

cos ⁡ θ = 1 2

Então θ varia de - 60 ° até 60 °

- π 3 ≤ θ ≤ π 3

Passo 4

Agora basta verificar se ela é diferenciável calculando sua derivada:

r → t = 4 cos ⁡ θ ,   4 sin ⁡ θ →             r ' t = - 4 sin ⁡ θ ,   4 cos ⁡ θ

Repare que essa derivada aí funciona para qualquer ponto. Então, sim, ela é diferenciável !

Resposta

r → t = 4 cos ⁡ θ ,   4 sin ⁡ θ ,     - π 3 ≤ θ ≤ π 3

Exercícios de Livros Relacionados

Para cada um dos seguintes pares de equações paramétricas, esboce a curva e determine a sua equação cartesiana.
Para cada um dos seguintes pares de equações paramétricas, esboce a curva e determine a sua equação cartesiana.
Esboçar as curvas seguintes, representando o sentido positivo de percurso. Obter uma parametrização da curva dada, orientada no sentido contrário.d) r → t = 2 cos 3 ⁡ t ,2 s e n 3 t , t ∈ 0 , π 2
Esboçar as curvas seguintes, representando o sentido positivo de percurso. Obter uma parametrização da curva dada, orientada no sentido contrário.b) r → t = t ,t + 2 ,4 - 2 t , t ∈ 0 ,1
Esboçar as curvas seguintes, representando o sentido positivo de percurso. Obter uma parametrização da curva dada, orientada no sentido contrário.a) r → t = 2 + 3 cos ⁡ t ,1 + 4 s e n t , t ∈ 0 ,2 π