Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Caso Escalar R²

Ver Teoria
Exercício 311234567891011121314151617181920212223242526272829303233343536373839404142434445464748495051525354555657585960

Enunciado

  1. Calcule a massa da elipse x 2 9 + y 2 4 = 1 , situada no primeiro quadrante, se a densidade em cada ponto é igual ao produto das coordenadas do ponto.

Passo 1

Ouvi falar em Massa?! Cara! Massa de curva, a essa altura do campeonato é dada por:

M a s s a   d e   c u r v a = ∫ C δ x ,   y d s

Onde C é a curva que estamos trabalhando e δ x ,   y é a função de densidade da curva, saca?

A densidade dessa curva nos foi dito que é o produto das coordenadas, logo:

δ x ,   y = x y

e

M a s s a   d e   c u r v a = ∫ C x y   d s

Mas como toda integral de linha, devemos seguir um passo a passo maroto:

  1. Parametrizar a curva C que estamos trabalhando
  2. Trocar os termos da função
  3. Encontrar o termo d s

Bora? :D

Passo 2

Sim, parametrizar a curva C , mas a pergunta mais ideal a fazer por enquanto é: quem é a C ?

Como o próprio enunciado disse, C é a elipse x 2 9 + y 2 4 = 1 centrada na origem:

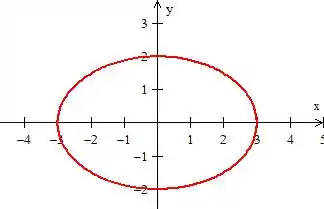
Porém só queremos o primeiro quadrante, então...

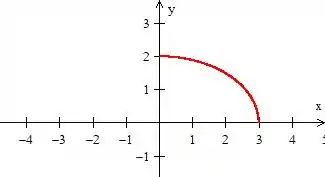
esse é o nosso C . Pegou?

Passo 3

Curva vista, podemos então continuar com a parametrização! Como estamos trabalhando com uma elipse do tipo x 2 a 2 + y 2 b 2 = 1 , podemos pensar em uma parametrização “elíptica”, onde sempre substituimos:

x = a cos ⁡ θ

y = b sin ⁡ θ

Como no nosso caso temos essa elipse aqui:

x 2 9 + y 2 4 = 1     →

x 2 3 2 + y 2 2 2 = 1

, a = 3 e b = 2 . Então:

x = 3 cos ⁡ θ

y = 2 sin ⁡ θ

ou, de uma forma mais elegante, a parametrização é

r θ = 3 cos ⁡ θ ,   2 sin ⁡ θ

Passo 4

Lembre-se que nunca devemos concluir uma parametrização sem antes dizer onde o parâmetro está variando, heim!

Nesse caso, como estamos lidando com um pedaço apenas no primeiro octante...

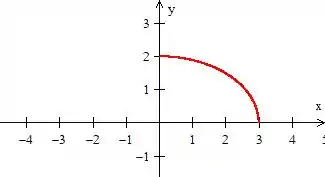
e lembrando que θ é sempre esse cara que sai do eixo x girando no sentido anti-horário, só podemos ter

0 ≤ θ ≤ π 2

Beleza?

Passo 5

Sendo assim, a nossa segunda função aqui é justamente mudar a função δ x ,   y = x y para os termos dessa parametrização (basta trocar esse x , y aí)

δ x ,   y = x y           →

δ r ( θ ) = 3 cos ⁡ θ ⋅ 2 sin ⁡ θ →

δ r ( θ ) = 6 cos ⁡ θ ⋅ sin ⁡ θ

Passo 6

Devemos agora encontrar o termo d s fazendo

d s = r ' ( θ ) d θ

Calculando essa derivada da parametrização r θ = 3 cos ⁡ θ ,   2 sin ⁡ θ ...

r ' ( θ ) = - 3 sin ⁡ θ ,   2 cos ⁡ θ

Extraindo o módulo desse vetor derivada

r ' ( θ ) = - 3 sin ⁡ θ 2 + 2 cos ⁡ θ 2

r ' ( θ ) = 9 sin 2 ⁡ θ + 4 cos 2 ⁡ θ

então

d s = 9 sin 2 ⁡ θ + 4 cos 2 ⁡ θ d θ

Passo 7

Retornando para a integral de linha que estamos trabalhando

∫ C x y   d s

e substituindo tudo...

∫ 0 π 2 6 cos ⁡ θ ⋅ sin ⁡ θ   9 sin 2 ⁡ θ + 4 cos 2 ⁡ θ d θ

Agora é só meter bronca e calcular essa integral aí, bora?:D

Bem, lembrando que sin 2 ⁡ θ = 1 - cos 2 ⁡ θ ...

∫ 0 π 2 6 cos ⁡ θ ⋅ sin ⁡ θ   9 sin 2 ⁡ θ + 4 cos 2 ⁡ θ d θ =

∫ 0 π 2 6 cos ⁡ θ ⋅ sin ⁡ θ   9 1 - cos 2 ⁡ θ + 4 cos 2 ⁡ θ d θ =

∫ 0 π 2 6 cos ⁡ θ ⋅ sin ⁡ θ   9 - 9 cos 2 ⁡ θ + 4 cos 2 ⁡ θ d θ =

∫ 0 π 2 6 cos ⁡ θ ⋅ sin ⁡ θ   9 - 5 cos 2 ⁡ θ d θ

se fizermos uma substituição do tipo

9 - 5 cos 2 ⁡ θ = u           →             d u = 10 cos ⁡ θ sin ⁡ θ   d θ       →

sin ⁡ θ cos ⁡ θ   d θ = d u 10

Não se esqueça dos limites:

θ = 0                 →                     u = 9 - 5 cos 2 ⁡ 0 = 4          

θ = π 2                 →                     u = 9 - 5 cos 2 ⁡ π 2 = 9          

∫ 0 π 2 6 cos ⁡ θ ⋅ sin ⁡ θ   9 - 5 cos 2 ⁡ θ d θ = ∫ 4 9 6   u d u 10 =

3 5 ∫ 4 9   u   d u =

3 5 2 3 u 3 2 4 9 =

3 5 2 3 u u 4 9 =

3 5 2 3 9 9 - 2 3 4 4 =

3 5 18 - 16 3 =

3 5 38 3 = 38 5

Resposta

38 5

Exercícios de Livros Relacionados

Calcule a integral de linha, onde C é a curva dada. ∫ C x + 2 y d x + x 2 d y C consiste nos segmentos de reta de ( 0,0 ) a ( 2,1 ) e de ( 2,1 ) a ( 3,0 ) .
Calcule o valor da integral de linha, onde C é a metade é a metade do círculo x 2 + y 2 = 16
Calcule a integral de linha, onde C é a curva dada.int_C x y^3 d s , C : x = 4 s e n t , y = 4 cos t , z = 3 t , 0 = t = (pi)/(2)
Determine o valor exato de ∫ C x 3 y 5d s , onde C é a parte da astróide x = c o s 3 t , y = s e n 3 t no primeiro quadrante.
Calcule a integral de linha, onde C é a curva dada.int_C x y^4 d s , C é a m e t a d e d i r e i t a d o c í r c u l o x^2 + y^2 = 16 é í