- Apresente uma parametrização diferenciável para as seguintes curvas planas:
Passo 1
Pow! É sempre muito recomendado que se desenhe a curva antes de parametriza-la.
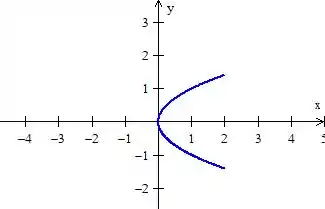
Esse caso é bem simples: nos representa uma parábola viradinha ao redor de :
Passo 2
Como está explicitamente em função de , podemos pensar em uma parametrização explícita onde podemos chamar de e ao mesmo tempo ganhamos :
Assim, uma parametrização é:
Como varia de a ...
Passo 3
Agora basta verificar se ela é diferenciável calculando sua derivada:
Repare que essa derivada aí funciona para qualquer ponto, em especial aos de . Então, sim, ela é diferenciável !
Resposta
Exercícios de Livros Relacionados
Para cada um dos seguintes pares de equações paramétricas, esboce a curva e determine a sua equação cartesiana.
Para cada um dos seguintes pares de equações paramétricas, esboce a curva e determine a sua equação cartesiana.
Esboçar as curvas seguintes, representando o sentido positivo de percurso. Obter uma parametrização da curva dada, orientada no sentido contrário.d) r → t = 2 cos 3 t ,2 s e n 3 t , t ∈ 0 , π 2
Esboçar as curvas seguintes, representando o sentido positivo de percurso. Obter uma parametrização da curva dada, orientada no sentido contrário.b) r → t = t ,t + 2 ,4 - 2 t , t ∈ 0 ,1
Esboçar as curvas seguintes, representando o sentido positivo de percurso. Obter uma parametrização da curva dada, orientada no sentido contrário.a) r → t = 2 + 3 cos t ,1 + 4 s e n t , t ∈ 0 ,2 π