Faça o gráfico das funções abaixo, encontrando alguns dos pontos pertencentes ao gráfico e tentando deduzir o restante. O objetivo aqui é mostrar que existe uma forma de fazer o gráfico de qualquer função, basta encontrarmos diversos pontos pertencentes ao seu gráfico. Obviamente, esse método é entediante, mas é importante utilizá-lo uma vez na vida. Ao longo desse curso, aprenderemos técnicas para encontrar o gráfico de certas funções sem precisar recorrer ao método desse exercício. Futuramente, em Cálculo , você aprenderá mais técnicas para traçar o gráfico de funções.
a) dada por
b) dada por
c) dada por
d) dada por
Passo 1
Fala, galera! Vamos resolver essa questão.
O enunciado nos deu algumas funções e pediu pra gente desenhar o gráfico delas.
Para isso, vamos encontrar os pontos do gráfico variando os valores de dentro do domínio dado. Vamos plotar esses pontos no plano cartesiano e verificar a curva da nossa função.
Vamos lá!
Passo 2
Na letra a), temos dada por . Nosso domínio e nosso contradomínio são os números reais e nossa lei de formação é .
Chutando alguns valores de dentro do domínio e substituindo na lei de formação para encontrar , temos a tabela:

Juntando esses pontos no plano cartesiano, temos:
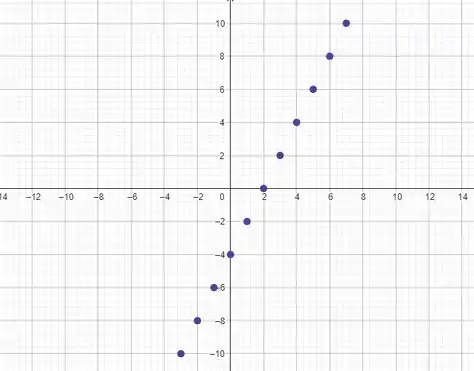
Daí, podemos deduzir que nosso gráfico é uma reta infinita, que passa por quando e por , quando . Temos:
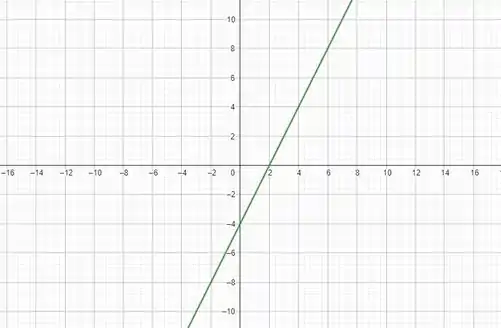
Passo 3
No item b), temos dada por .
Nossa lei de formação é igual a função do passo anterior, mas o nosso domínio agora está apenas no intervalo . Então, os valores de vão variar apenas de até , mas sem incluir o , porque o intervalo é aberto nesse ponto.
Variando , temos a tabela:

Plotando esses pontos no plano, temos:
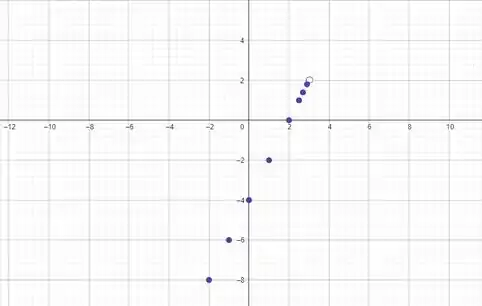
Repare que a bolinha é aberta em , porque o domínio da função não está definido nesse valor. Juntando tudo, temos nossa reta:
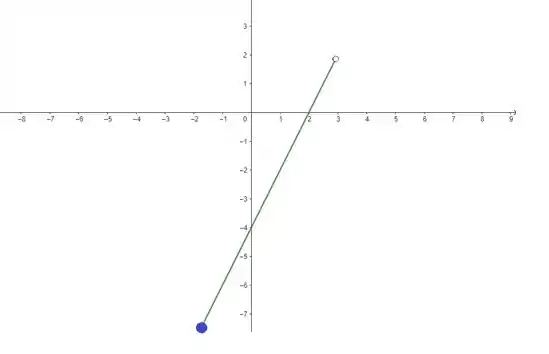
Passo 4
Na letra c), temos dada por .
Galera, repara que independentemente do valor de , o valor de vai ser sempre , não vai alterar a função. Isso significa que a nossa função é constante e plotando no gráfico nós temos:
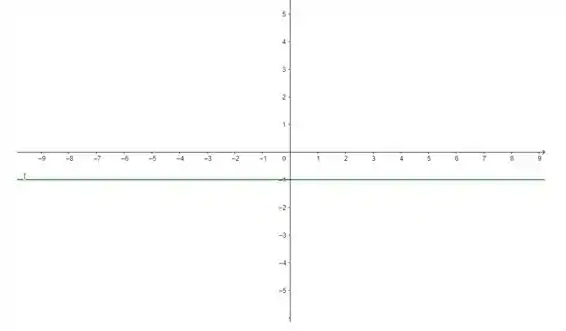
Passo 5
Na letra d), temos dada por . Variando os valores de , montamos a tabela:

Colocando esses pontos no plano cartesiano, temos:
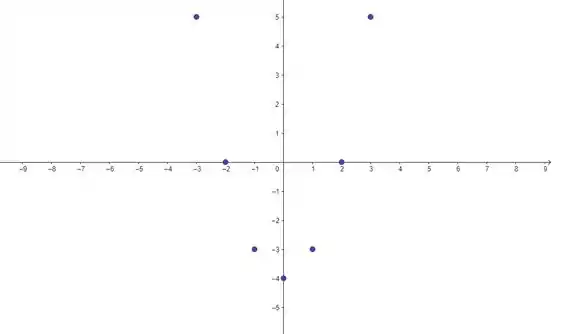
Juntando esses pontinhos, temos nossa curva:
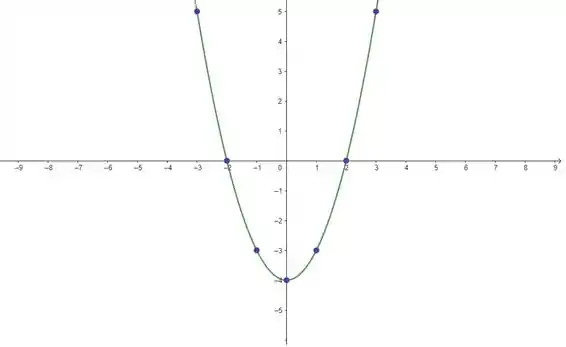
Prontinho, galera! Até a próxima! 😉