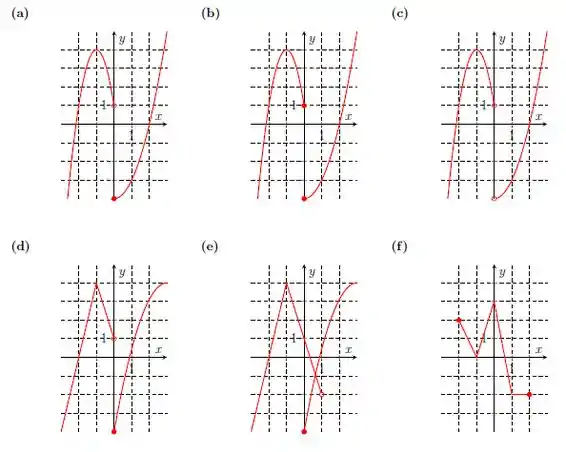
Diga quais dos gráficos abaixo representam alguma função. Nos casos que são funções, determine o domínio.
Passo 1
Fala, galera! Vamos resolver essa questão.
O enunciado nos deu alguns gráficos e pediu pra gente verificar quais deles representam uma função, e nos casos que forem funções, determinar o domínio.
Galera, podemos verificar pela representação cartesiana se é ou não funç��o, verificando se a reta paralela ao eixo iniciando no ponto , em que pertence ao domínio, encontra sempre o gráfico de em um só ponto. Então, vamos traçar retas paralelas nos gráficos e determinar o conjunto de todos os valores possíveis para , que definem o domínio.
Vamos lá!
Passo 2
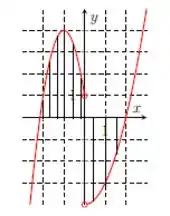
Olhando o gráfico da letra a), temos:
Repare que a gente traçou retas paralelas ao eixo e que todas as retas encontram o gráfico de em um só ponto, pra e . Em , repare que apenas o ponto está definido, porque em cima a gente tem uma bolinha aberta.
Sendo assim, temos uma função, nosso domínio são todos os valores possíveis de , nesse caso temos:
Passo 3
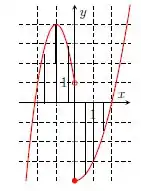
Na letra b), temos:
Repare que no ponto , na reta , a curva mostra dois pontos definidos. Então, a reta vertical encontra o gráfico em dois pontos. Isso significaria que teriam dois valores de para um único valor de no domínio, o que não pode acontecer. Por isso, não é função.
Passo 4
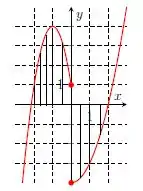
Na letra c), temos:
Repare que agora a reta paralela no ponto não encontra nenhum valor em , porque temos duas bolinhas abertas. Isso significa que o gráfico não está definido naquele ponto. Como não podemos ter pontos do domínio sem um valor correspondente no contradomínio, o gráfico não representa uma função.
Passo 5
Na letra d), traçando retas paralelas ao eixo , temos:
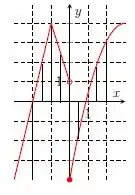
Repare que para de até , as retas encontram o gráfico em apenas um ponto. Para de até , as retas também encontram o gráfico em um único ponto. Em , temos uma bolinha aberta e uma bolinha fechada em , então o gráfico está definido no ponto , dessa forma, a reta também encontra o gráfico em único ponto. Ela é uma função e temos o domínio:
Passo 6
Na letra e), temos:
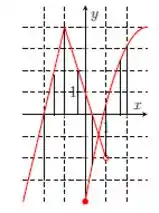
Repare que depois a reta paralela a cruza o gráfico em dois pontos, portanto, não é função.
Passo 7
Na letra f), temos:
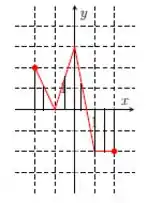
Aqui nossas retas paralelas encontram o gráfico em apenas um ponto, para variando de a . Então, o gráfico representa uma função e o nosso domínio é definido no intervalo fechado:
Prontinho, galera! Até a próxima! 😉
Resposta
Com domínios respectivos: