UFSC, Sem Campus, Pré-Cálculo, Listas Pré Cálculo - Lista 10, Questão 3
Diga quais dos conjuntos abaixo representam uma função com domínio e contradomínio . Nos casos que são funções, determine o conjunto imagem.
(a)
(b)
(c)
(d)
(e)
(f)
(g)
Passo 1
Fala, galera! Vamos resolver essa questão.
O enunciado nos deu uma função cujo domínio é o conjunto e cujo contradomínio é o conjunto dos números inteiros, . Ele pediu pra gente verificar quais dos conjuntos de a representam essa função e determinar o conjunto imagem.
Galera, para que seja uma função todos os elementos do domínio precisam ter um correspondente no contradomínio. A gente não pode ter um elemento no conjunto que não tenha correspondente ou que tenha mais de um correspondente no conjunto .
Como o nosso domínio já foi definido, vamos olhar nos conjuntos de pares ordenados , onde os elementos do domínio aparecem como . E o nosso contradomínio, representado por , vai ter somente números inteiros, não fracionários, beleza?
Vamos lá!
Passo 2
Lembrando, nosso domínio são todos os valores que pode assumir, no caso . Olhando para o conjunto :
Vamos pegar os elementos nos pares ordenados . Temos:
Que é igual ao nosso conjunto . Até aí tudo certo, agora vamos ver o contradomínio:
São todos números inteiros. Cada elemento do domínio tem apenas um correspondente no contradomínio, então o conjunto representa nossa função e tem imagem .
Passo 3
No item b), temos:
Vamos desenhar um diagrama de flechas pra ficar mais claro a relação entre os pares ordenados:
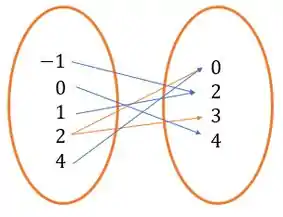
Repare que tem duas flechas saindo do . E para que seja uma função todos os elementos do domínio precisam ter um único correspondente no contradomínio. Então, o conjunto não é função.
Passo 4
Na letra , temos:
Na posição , temos: , e na posição temos: . Definimos o nosso domínio . Cada elemento do domínio possui um único correspondente em . Então, temos uma função, cuja imagem é igual ao contradomínio .
Mas o domínio dessa função não contém todos os elementos do conjunto , então não satisfaz a nossa condição.
Passo 5
Na letra , temos:
Onde definimos o domínio , que é igual a . Cada um dos elementos do domínio tem apenas um elemento correspondente no contradomínio, que também é a imagem , que pertence aos números inteiros. Então, ela representa nossa função.
Passo 6
Na letra , temos:
O domínio é também. E o contradomínio é , que não faz parte do conjunto dos números inteiros, porque possui um número fracionário. Portanto, não representa nossa função.
Passo 7
Em , temos:
Que tem por domínio que é diferente do nosso conjunto . Além disso, sua imagem é dada por , que também não pertence aos números inteiros, portanto, também não representa nossa função.
Passo 8
Em , temos . Repare que os elementos de pertencem ao conjunto , então podemos definir o domínio . A imagem é dada por , então:
Que são todos números inteiros, logo, representa nossa função.
Valeu, galera! Até a próxima! 😉