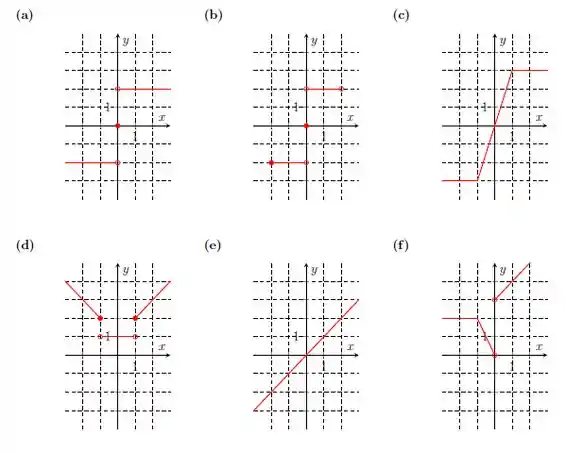
Os gráficos abaixo representam funções. Determine o domínio e a imagem de cada uma delas.

Olhando o gráfico da letra a), temos:

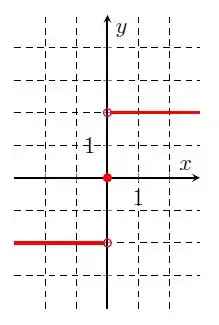
Repare que de até , temos uma reta no terceiro quadrante, mas em ela tem uma “bolinha aberta”, o que significa que ela não tá definida naquele ponto. Olhando a origem do gráfico, a gente vê que existe um ponto definido , que tá com a “bolinha fechada”. Em seguida, a gente passa a ter outra reta para os valores positivos de .

Então, como nosso domínio são todos os valores possíveis de e como está definido para todos os valores reais no gráfico, temos:

A imagem vão ser todos os valores que o vai atingir no . Observe que no intervalo , a função varia em , depois ela passa pelo ponto e segue variando em . Então, nossa imagem é:

Na letra b), temos:

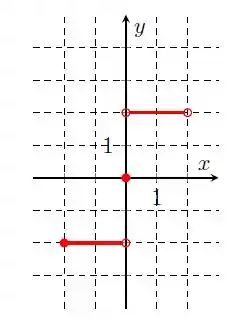
Repara que agora tá vindo de até , com uma bolinha aberta, depois ele pula pra e segue em outra reta de até . A gente só precisa ter atenção pra colocar o intervalo aberto onde a gente tem a bolinha aberta e o intervalo fechado na bolinha fechada. Assim, nosso domínio fica:

A imagem são todos os valores de que a função atinge, então temos:

Na letra c), temos:

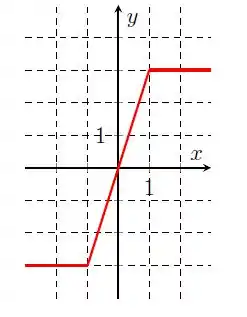
Olhando o gráfico, a gente percebe que nossa função agora tá definida para todos os valores de . Então, temos o domínio:

E nossa imagem, que representa os valores de , será:

Na letra d), temos:

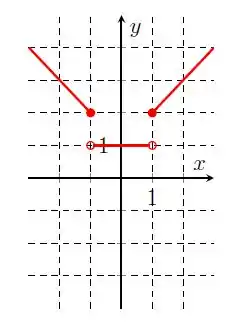
Repare que primeiro temos vindo de até , depois temos uma reta horizontal de a , e em seguida, o gráfico muda, variando de a . Juntando tudo, vemos que pode assumir qualquer número real e temos o domínio:

E nossa imagem, que representa os valores de , será:

Na letra e), temos:

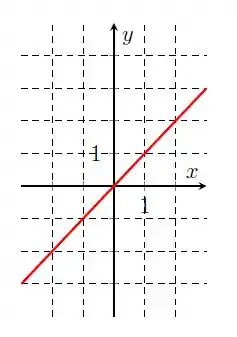
Temos uma reta infinita, que pode assumir qualquer valor real em e , então:

Na letra f), temos:

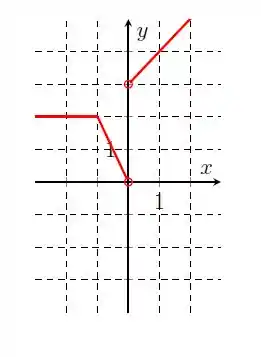
Temos vindo de até , onde a função não tá definida, por temos uma bolinha aberta. Depois, a função continua de , sem incluir o zero, até . Então, temos o domínio:

Para , nós temos um patamar em , depois uma reta decrescente até , sem incluir o zero. Em seguida, temos uma reta crescente de a . Logo,

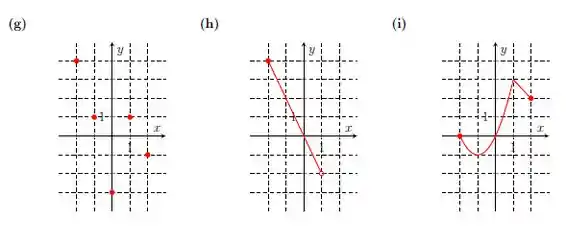
Em g), temos:

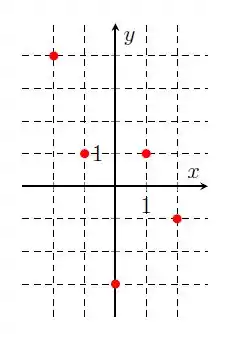
Temos os pontos . Logo, nosso domínio é definido por:

E nossa imagem, por:

Em h), temos:

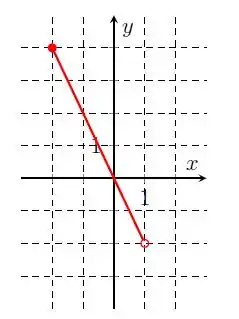
Nossa reta tem os valores de variando de até , sem incluir o . E variando de até . Logo, temos o domínio:

E a imagem:

Em i), temos:

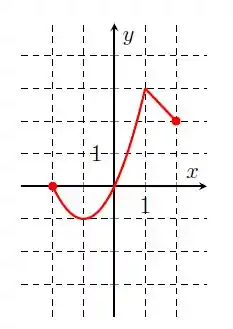
Aqui tá variando de até , então nosso domínio será:

E para os valores de , temos a imagem:

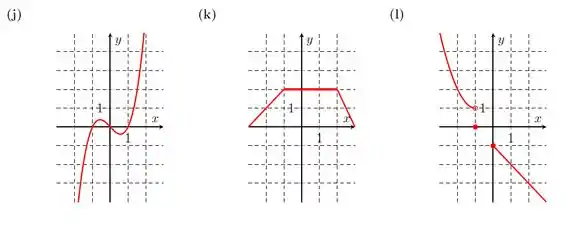
Na letra j), temos:

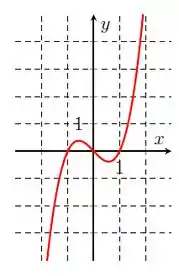
Repara que nosso tá variando de até . Então, temos o domínio:

E nossa imagem vai de a , então:

Na letra k), temos:

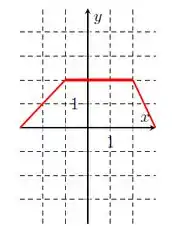
Onde tá indo de a . Logo,

E nosso vai de até , então:

Na letra l), temos:

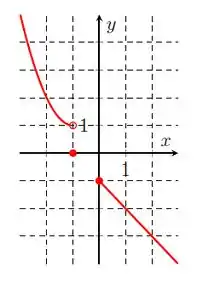
Repare que nós temos uma função por partes, onde vem de atá , sem incluir o , depois passa pelo ponto , e segue do ponto até . Então, nosso domínio será:

E nosso varia de até , depois , e segue de até . Então, nossa imagem será:

Prontinho, galera! Até a próxima! 😉