UFSC, Sem Campus, Pré-Cálculo, Listas Pré Cálculo - Lista 10, Questão 20c.
20. Para cada uma das funções abaixo, determine o domínio, calcule (se pertencer ao domínio), faça o gráfico e determine o conjunto imagem.
c)
Passo 1
Iae, como vai? Essa questão está um pouco complicada? Fique tranquilo que vamos tentar te ajudar. 😎👍
Nessa questão queremos obter o conjunto domínio e o conjunto imagem da função além também do seu gráfico e da sua imagem em (se possível).
Muitas coisas, não é? 👀
Podemos dizer que o conjunto imagem e o conjunto com os possíveis valores que a função pode assumir como resultado, ou seja, os possíveis valores de . Já o conjunto domínio podemos dizer que são os possíveis valores que a função pode assumir como entrada, ou seja, os possíveis valores para .
Para obter o gráfico de podemos plotar alguns pontos e estimar como será o comportamento da função.
E por último, calculamos na função para ver se existe uma imagem correspondente.
Entendeu? Bora começar! 😊
Passo 2
Analisando a função, vemos que para ela assume um valor constante e igual a . Já entre a função assume o valor da reta e para ela volta a assumir uma constante .
Portanto, podemos dizer que a imagem de são os valores qua a função assume em entre e e as constantes e .
Já para o domínio, vemos que não há nenhuma restrição para entradas para valores de , portanto
Tranquilo até aqui? 😎
Passo 3
Para obter o gráfico de , fazemos uma reta paralela ao eixo em para e outra em para .
Além disso entre , esboçamos a reta .
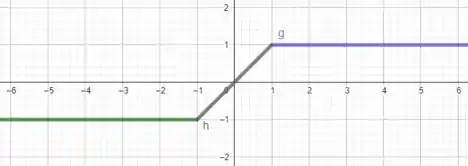
Com isso, podemos ver que em a função assume valor , portanto
E todos viveram felizes para sempre. Fim! 😉 Entendeu tudo? Responde Aí
