Em cada caso abaixo, expresse a(s) condição(ões) dadas em termos de equações ou inequações envolvendo valores absolutos e determine os respectivos conjuntos solução.
A diferença entre as distâncias de a e é exatamente igual a
Passo 1
A ideia de distância entre números reais é a nossa ideia de módulo.
Então a distância de à vai ser
Enquanto a distância de à vai ser
Passo 2
Ele disse que A diferença entre as distâncias de a e é exatamente igual a .
Isso quer dizer que se subtrairmos as distâncias, devemos ter exatamente
Essa vai ser a nossa Equação.
Passo 3
Precisamos fazer os dos módulos e ver como será a expressao, primeiro vamos pegar módulo
Resolvendo aquela inequação, vamos ter
E
Resultando em
Passo 4
Vamos para o módulo
Resolvendo aquela inequação, vamos ter
E
Resultando em
E vamos ter
Passo 5
Vamos agora juntar todos esses módulos
Temos que olhar os intervalos primeiro, para entendermos como vai ficar
Então, no fundo temos
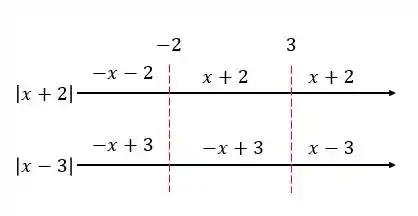
Fazendo a soma, vamos ter
Vai ficar
Vamos ter equações para resolver em cada letra.
Passo 6
Com
Mas isso é verdadeiro para qualquer valor do intervalo, então a solução vai ser
Em forma de intervalo
Passo 7
Com
Esse valor não está no intervalo, então não teremos solução aqui
Passo 8
Com
Mas isso é falso para qualquer valor do intervalo, então não teremos solução aqui
A nossa solução vai ser