Nos exercícios a , resolva para e represente a solução na reta numérica.
19.
Passo 1
Oi, galerinha! Tudo bom? Aqui temos uma inequação com módulo dos dois lados para resolver!
Mas antes podemos dar uma ajeitada nela para deixar ela mais fácil de ser resolvida!
Passando tudo que é para um lado só, ficamos com
Mas como temos uma inequação do tipo,
Para resolver é só escrever as duas inequações e achar a união dessas inequações
e
Beleza?! Então ficamos com,
Passo 2
Vamos começar resolvendo a primeira
Passando o para esquerda
Temos que juntar essa parada toda
Precisamos analisar o sinal das duas funções, tanto no numerado como no denominador.
Passo 3
Para o numerador temos,
Para o denominador, ficamos com
Com isso, ficamos com,
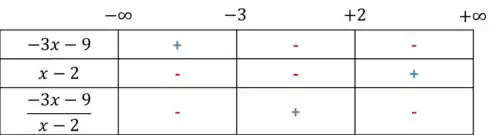
Logo,
ou
Passo 4
Vamos para a segunda inequação
Passando o para direita
Temos que juntar essa parada toda, e vamos escrever com o sinal ao contrario da desigualdade
Precisamos analisar o sinal das duas funções, tanto no numerado como no denominador, como passo anterior. O quadro ficará assim:
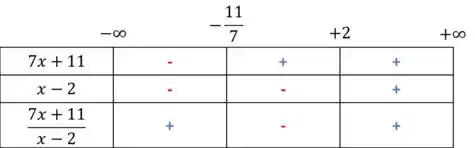
Logo,
ou
Passo 5
Agora temos a solução de cada uma dessas inequações, a parada é achar a interseção dessas duas soluções
ou ou
Assim, a nossa solução vai ser entre aqueles cara bonitinhos,
ou
Resposta
ou