Seja .
a) Determine o domínio da função, expresse sem usar módulo e esboce o seu gráfico.
c) Encontre todos os valores de tais que .
Passo 1
a)
O domínio da função módulo é , então a função não tem nenhum tipo de restrição e o domínio dela também é .
Passo 2
Agora vamos tirar o módulo da .
Repare que para , e para , então vamos estudar a função nos intervalos e .
Passo 3
Quando, temos:
Logo:
Então, nesse caso a função é:
Passo 4
Quando :
Logo:
Então nesse intervalo a função é:
Passo 5
Finalmente, quando :
Portanto:
Então a é:
Passo 6
Concluímos que a função pode ser escrita assim:
Passo 7
E o gráfico dela é:
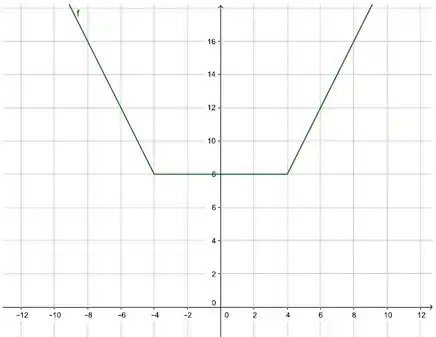
Passo 8
c)
Na letra (a) vimos que
nunca é maior que (não me diga), então vamos ver para que valores de temos ou :
Portanto, temos para .
Resposta
a)
Domínio da :
escrita sem módulo:
Gráfico:
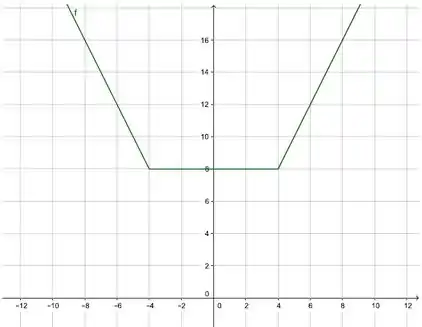
c)