Determine a solução na inequação abaixo
Passo 1
De novo caímos naquela situação de inequações modulares com dois módulos, podemos resolver daquela forma que fizemos nos exercícios anteriores, mas é mais fácil dar uma manipulada nisso e transformar em um módulo só. Diferente do outro exercício que é mais tranquilo fazer da forma tradicional.
Vamos começar arrumando isso do lado direito,
Vamos passar aquele módulo de para a esquerda multiplicando, mas lembrando que ele nunca pode ser , assim já temos que excluir da nossa solução o , mais tarde vamos relembrar desse detalhe que vai ser importante.
Passando ele para o outro lado vamos ter
Arrumando isso
E passamos a ter um único módulo. Aqui temos a inequação modular menor ou igual, assim temos que achar a interseção das soluções das inequações abaixo
Passo 2
Vamos começar resolvendo a primeira
Passando o para esquerda
Temos que juntar essa parada toda
Precisamos analisar o sinal das duas funções, tanto no numerado como no denominador.
A do denominador é de boa, vamos ter ela positiva depois de e negativa antes.
A função de segundo grau precisamos do gráfico para isso, e para o gráfico precisamos das raízes
Isso nos diz que essa função não tem raízes, o seu gráfico vai ficar
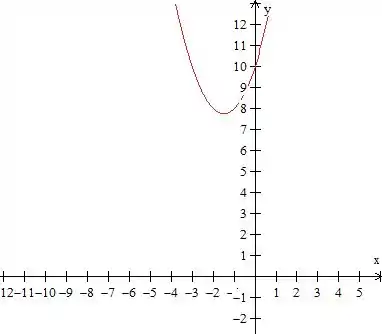
Podemos ver que ele sempre vai ser positivo. Vamos fazer o quadro de sinais.
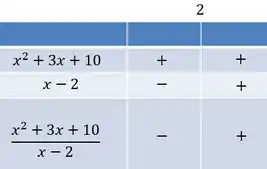
Queremos essa fração sendo negativa, então vamos pegar a parte menor que
Repara que a expressão tem menor ou igual, e aqui eu só coloquei menor. Isso porque o é raiz do denominador, e ele não pode ser , então precisamos excluir o
Passo 3
Vamos para a segunda inequação
Passando o para direita
Temos que juntar essa parada toda, e vamos escrever com o sinal ao contrario da desigualdade
Precisamos analisar o sinal das duas funções, tanto no numerado como no denominador.
A do denominador é de boa, vamos ter ela positiva depois de e negativa antes.
A função de segundo grau precisamos do gráfico para isso, e para o gráfico precisamos das raízes
Isso nos diz que essa função tem duas raízes,
E
O seu gráfico vai ficar
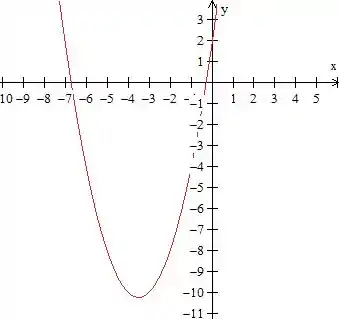
Podemos ver que entre as raízes ele vai ser negativo, e na outra parte vai ser positivo. Vamos fazer o quadro de sinais.
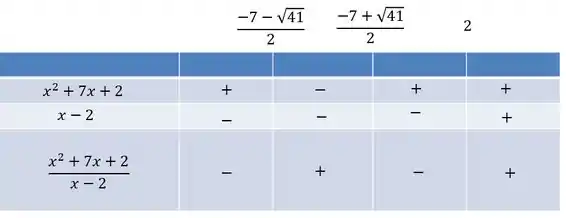
Queremos essa fração sendo positiva, então vamos pegar
Aqui de novo temos que excluir o , pelo mesmo motivo de antes, ele é raiz do denominador
Passo 4
Agora temos a solução de cada uma dessas inequações, a parada é achar a interseção dessas duas soluções
Assim, a nossa solução vai ser entre aqueles cara bonitinhos,