Estude a variação do sinal das funções dos exercícios 26. A 29.
28.
Passo 1
Oi, galerinha! Tudo bom? Aqui nós temos que fazer o estudo do final da seguinte função:
Repara que ele é o produto e divisão de vários polinômios do primeiro grau. Então o que vamos fazer aqui é realizar o estudo do sinal de cada termo (ou seja, verificar quando essa porção é positiva e quando ela é negativa) e depois multiplicar os sinais para ter o estudo da função como um todo.
Bora lá!
Passo 2
Começando pelo primeiro termo,
Ou seja, a função é negativa para e positiva para .
Já o segundo termo é uma módulo
Então pela definição de módulo podemos considerar que ele é positivo para qualquer
Por fim, o termo,
Temos que a função é negativa para e positiva para .
Bora organizar esses dados?
Passo 3
Para organizar esses dados numa tabela preenchendo tudo com sinal de cada função. Ficará assim:
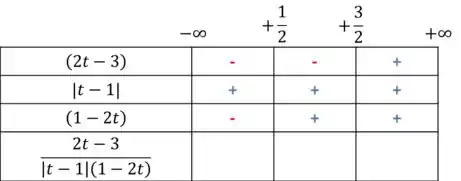
Então, galerinha, essa tabela sumariza quando cada termo é positivo ou negativo, baseado nos valores encontrados no passo anterior.
Agora, para preencher a ultima linha e completar o estudo do sinal, vamos ter multiplicar os sinais de cada linha.
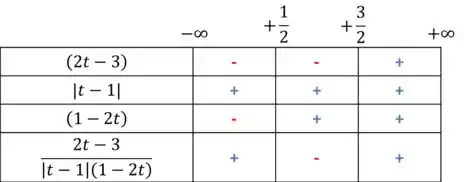
Prontinho! A função é positiva para os intervalos e e negativa em .
Resposta
- Positiva em e .
- Negativa em .