UFJF. Equações Diferenciais I. Lista 2022.2. Questão 4b.
4. Verifique se cada uma das afirmações abaixo é verdadeira ou falsa. Justifique
provando as verdadeiras e apresentando um contra-exemplo para as falsas.
(b) Sejam e duas sequências tais que, para todo , temos
. Se é convergente então é convergente.
Passo 1
Iae, meus queridos! Está com dificuldades nessa questão? Não se preocupe! Estamos aqui para ajudar 😉
Nessa questão, temos algumas afirmações e nosso objetivo é provar que tal afirmação é verdadeira ou falsa.
Nesse caso, a afirmação nos diz que se temos duas sequências e e é menor que , então se é convergente, logo é convergente.
E então! O que você acha?? 🤔
Podemos imaginar duas sequências e em que seja maior de para todo e que faça a afirmação ser falsa?
Bora ver! 😉
Passo 2
Se considerarmos como uma sequência convergente dada por .
Sabemos que essa sequência converge, pois, seu limite tende a uma constante
Como tende a um valor muito grande, tende a um valor muito pequeno, muito próximo de , logo
Assim, vemos que é convergente.
Agora vamos imaginar uma sequência que seja menor que para todo natural.
Que tal a sequência ? dessa forma, como está contida no primeiro quadrante e no segundo quadrante, então .
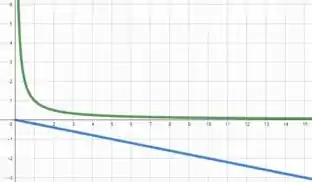
Dessa forma, calculando o limite de , temos
Quando tende ao infinito temos um numero muito grande dividido por um numero significativamente menor, então
Como o limite de resultou em , então diverge!
Portanto, a afirmação do enunciado não é verdadeira em todos os casos.
É isso, espero ter ajudado! Entendeu tudo? Responde Aí! 😎👍
Resposta
Falsa