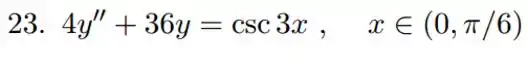
Passo 1
Vamos lá resolver essa EDO. Ela não é homogênea e essa função chatinha aí do outro lado da equação complica não é lá muito simples. Então vamos resolver usando o método da variação de parâmetros. De qualquer forma a primeira coisa é resolver como se fosse homogênea.
Determinando a equação característica
E encontrando as raízes temos
Que nos leva a uma solução homogênea
Passo 2
Temos
No método da variação de parâmetros precisamos supor uma solução particular que seja
No nosso caso
Para calcular precisamos primeiro encontrar
Calculando
Passo 3
Agora vamos calcular
No nosso caso
Então
Daí
Falta calcular
Passo 4
Então nossa solução particular é
E como sabemos que
Então
Resposta
Exercícios de Livros Relacionados
Resolva a equação diferencial usando o método da variação de parâmetros. y ' ' - 2 y ' + y = e x 1 + x 2
Resolva a equação diferencial usando Coeficientes indeterminados eVariação de parâmetros. y ' ' - y ' = e x
Resolva a equação diferencial usando o método da variação de parâmetros. y ' ' + 4 y ' + 4 y = e - 2 x x 3
Em cada um dos problemas de 29 a 32, use o método esquematizando no Problema 28 para resolver a equação diferencial dada. t 2 y ' ' - 2 t y ' + 2 y = 4 t 2 , t0 ; y 1 t = t
Em cada um dos problemas de 29 a 32, use o método esquematizando no Problema 28 para resolver a equação diferencial dada. 1 - t y ' ' + t y ' - y = 2 t - 1 2 e - t , 0t1 ;y 1 t = e t (veja o Problema