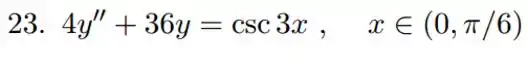Exercícios de Método da Variação dos Parâmetros - Lista de Exercícios Resolvida

Determine a solução geral da equação

Sabendo-se que são soluções linearmente independentes para em ,

1. Encontre a solução particular para:
2. Dê a equação solução geral para a equação e defina um intervalo para que esta seja válida

Sabendo-se que formam um conjunto fundamental de soluções para em , encontre a solução geral para:

Dada a equação diferencial de segunda ordem ,

1. Usando o método dos coeficientes a determinar resolva o problema de valor inicial
2. Resolva a equação diferencial

Determine a solução geral da equação

Determine a solução geral da equação

3)a - Resolva a equação , .

b - Determine uma solução particular da equação , .

Sugestão: a equação de Euler pode ser reduzida a uma EDO com coeficientes constantes através da substituição .

Teste 2: Analise as seguintes afirmações:

1. Se duas funções deriváveis são linearmente dependentes, as suas derivadas também são.
2. O determinante Wronskiano de duas funções quaisquer , é nulo em um ponto se, e somente se, as funções são linearmente dependentes.
3. Se uma equação diferencial de ordem possui o fator integrante , então a equação , define todas as soluções da equação.
4. Existe uma equação do tipo com funções contínuas em , tendo como soluções e .

São verdadeiras:

1. Apenas .
2. Apenas .
3. Apenas .
4. Apenas .
5. Apenas .

a) Resolva a equação de Euler-Cauchy: b) Use o método das variações dos parâmetros para resolver a seguinte equação:

Encontre todas as soluções da EDO:

Determine a solução geral da equação diferencial:

Usando o método da variação dos parâmetros, determine a solução geral da equação diferencial:

1. Encontre a solução da equação diferencial
2. Encontre a solução da equação diferencial

Considere a equação diferencial de segunda ordem, homogênea,

Resolva a equação diferencial não homogênea.

Encontre a solução geral da seguinte equação diferencial, utilizando o método de variação dos parâmetros.

Obtenha a solução geral da EDO:

(a) Determine a solução geral da equação

(b) Determine a solução do problema de valor inicial

Considere a seguinte EDO de ordem ,

Encontre a solução geral da equação homogênea associada, sabendo que é uma solução da equação homogênea. (Dica: Dado uma EDO , o teorema de Abel fornece uma maneira de calcular pela fórmula explícita para o Wronskiano ).

Usando o método da variação dos parâmetros, determine a solução particular da equação não homogênea.

Encontre a solução geral da equação diferencial

Encontre a solução geral da equação linear não homogênea abaixo

sabendo que a solução geral da equação homogênea associada é

Questão 1: Sabendo que e são soluções da equação linear homogênea,

Encontre a solução geral da equação diferencial não homogênea

Questão 2: Considere a equação diferencial de segunda ordem. Homogênea,

1. Resolva a equação diferencial não homogênea,

Determine a solução geral da equação

Resolva a equação de Euler abaixo.

Resolva a equação não homogênea abaixo via variação de parâmetros. (Obs: a homogênea associada está no item ).

Seja . Para resolver a equação não homogênea , por variação de parâmetros, é necessário conhecer duas soluções linearmente independentes da equação homogênea associada. Suponha que a solução de seja conhecida, e que não se anule no intervalo .

1. Prove que a outra solução de pode ser dada pela fórmula , onde , e é um ponto em .
2. Mostre que e são linearmente independentes em .

a) Resolva a equação de Euler-Cauchy:

b) Use o método das variações dos parâmetros para resolver a seguinte equação:

Considere um circuito RLC onde a força eletromotriz é , a resistência é , a indutância é e a capacitância é . Pela segunda Lei de Kirchoff, a carga q(t) no capacitor satisfaz

a) Determine a solução geral da homogênea.

b) Determine a solução geral da não homogênea.

c) A carga no circuito tende a zero quando t cresce?

d) Determine a carga q(t) do capacitor se a carga inicial é q(0) = 0 e a corrente inicial é q’(0) = 1.

Considere um sistema MMA onde a força externa é F(t) = e −t , a massa é m = 1, a constante de amortecimento é b = 2 e a constante da mola é k = 1. Pela segunda Lei de Newton, a posição y(t) da massa em relação ao equilíbrio satisfaz

a) Determine a solução geral da homogênea.

b) Determine a solução geral da não homogênea.

c) A posição da massa tende a zero quando t cresce?

d) Determine a posição y(t) da massa se a posição inicial é y(0) = 1 e a velocidade inicial é y’(0) = 0.

Considere a equação diferencial:

Mostre que e são soluções linearmente independentes calculando o Wronskiano.

Dado que e de são soluções da equação homogênea associada, utilize o método da variação de parâmetros para calcular uma solução particular da equação diferencial.

Considere a equação diferencial

Dado que a solução complementar de (*) é , use o método de variação dos parâmetros para encontrar uma solução particular da equação (*).