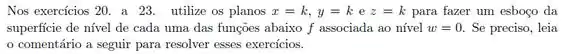
Passo 1
Precisamos encontrar a superfície de nível na nossa função .
Vamos então igualar nossa função a zero.
Que é a função modular que a gente tá acostumado, só que no plano .
Passo 2
Beleza, mas acontece que nossa função é uma função de 3 variáveis, de modo que temos que ter uma superfície de nível de espaço e não só uma curva no plano.
Aí que a gente usa a dica que a questão deu pra gente.
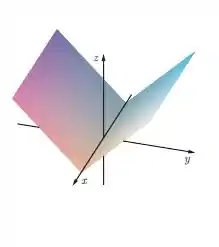
Pra encontramos a superfície a partir da curva, o que temos que fazer é traçar, em cada ponto da curva, uma reta perpendicular ao plano onde a curva se encontra, no caso, ao plano .
Assim, ao traçarmos uma reta perpendicular ao plano em cada ponto da curva, temos um cilindro em forma da função modular no espaço:
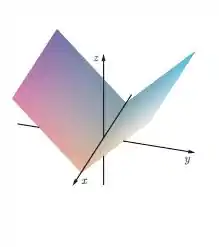
Resposta
Exercícios de Livros Relacionados
Calcule, caso exista.d) underset((x , y) - (0,0))(l i m) (x y)/(x^2 + y^2)
Calcule underset((h , k) - (0,0))(l i m) ((f (x + h , y + k) - f (x , y) - 2 x h - k))/(‖(h , k)‖) , onde f (x , y) = x^2 + y^2
1 - Calcule caso existae ) underset((x , y) - (0 , 0))(lim) (x y (x - y))/(x^4 + y^4)
Calcule, caso exista.b) underset((x , y) - (0,0))(l i m) (x)/(sqrt(x^2 + y^2))
Represente graficamente e o domínio da função z = f x , y dada por b) f x , y = 1 - z