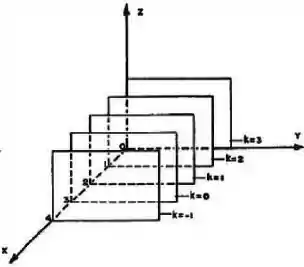
Na figura estão representadas superfícies de nível da função . Escreva uma expressão adequada para .
Passo 1
De cara essa questão pode parecer meio bizarra, mas vamos destrinchar ela com calma.
Primeiro: essas superfícies são superfícies de nível da função, portanto elas são dadas pela equação geral
com variando de a , como podemos ver na figura.
Passo 2
Outra coisa: podemos ver que essas superfícies são planos paralelos ao plano , portanto planos de equação
Vou chamar essa nova constante de (nome bem original, eu sei). Se você prestar bem atenção na figura, vai ver que os valores de estão indicados no eixo. E esses números são justamente os valores de , variando de a .
Portanto, as 5 superfícies de nível mostradas têm equação dada por:
Passo 3
Beleza, agora o lance é comparar os com os . Por exemplo, no primeiro plano lá atrás, de equação , temos . Ou seja:
Ou seja, já podemos escrever uma expressão não muito profissional pra :
Certo? Já que quando , vale 3.
Passo 4
Vamos ver um dos outros planos pra ter mais informações sobre . Por exemplo a superfície de nível . Ela corresponde ao nível .
Opa, se vale zero então
Hmm, e justamente o vale . Já dá pra ter um palpite:
O que você acha? Isso dá certo pro que vimos antes.
O jeito é testar pras outras superfícies de nível!
Passo 5
Vamos pegar a superfície
Temos
Pelo nosso palpite, isso daria
Os valores estão batendo! E se a gente parar pra olhar as outras superfícies de nível, podemos ver que conforme o vai crescendo, o vai diminuindo linearmente, e vice-versa.
Então é isso mesmo, na base do “chute direcionado” achamos uma expressão adequada pra função: