USP, Sem Campus, Cálculo 2, Listas de Cálculo 2 - USP, Politécnica - Lista 5 - Curvas no R3, Superfícies de Nível, Questão 2.1a
2.1. Em cada caso, esboce a superfície de nível da função :
a. .
Passo 1
Iae, meus queridos! Está com dificuldades nessa questão? Não se preocupe! Estamos aqui para ajudar 😉
Nesse problema, queremos esbo��ar a superfície de nível da função .
Tem alguma ideia de como fazer isso? 😁
Para esboçar uma superfície de nível de uma função , temos que igualar a onde representa o nível que vamos obter.
Dessa maneira, eliminamos uma dimensão da função e assim é possível esboçar a superfície formada no espaço tridimensional.
Sacou? Bora começar! 😉
Passo 2
Igualando a temos
Estamos interessados na superfície do nível , ou seja
Isolando em um lado da igualdade
Como e são de ordem , a superfície é dada por um plano que corta o eixo em , o eixo em e em
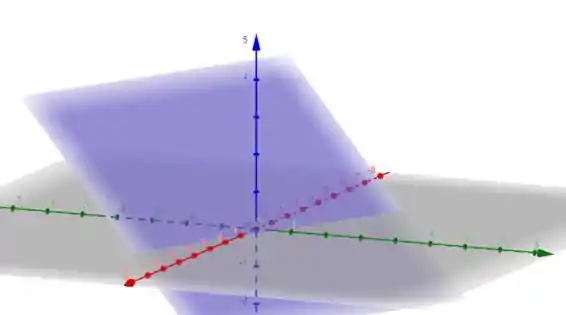
É isso, espero ter ajudado! Entendeu tudo? Responde Aí! 😎👍