UTFPR – Cálculo 2 – P1 2021.1 – Questão 2
Esboce as superfícies de nível da função dada por para
Passo 1
E aíí pessoal, tudo certinho? Vamos lá arrebentar nessa questão
O exercício deu uma função de 3 variáveis:
E aí queremos encontrar as superfícies de nível quando e
Para encontrarmos as equações que determinam as superfícies de nível, vamos fazer isso olha:
Para cada um dos 3 valores de k.
E aí precisamos lembrar lá das equações de superfícies que vemos em geometria analítica pra conseguirmos entender qual figura cada superfície vai representar ok?
Então vamos começar fazendo essa igualdade da função com cada um dos valores de
Passo 2
Para , vamos ter
Opa, não tem como uma exponencial elevada a alguma coisa ser igual a zero!! Repara que não tem nenhum valor tal que
Então, não temos superfície de nível pra , beleza?
Passo 3
Para , vamos ter
Como , temos
Legal, as bases são iguais, então podemos igualar os expoentes
Então:
Opa, lembrando lá de geometria analítica, isso é a equação de um cone elíptico ao longo do eixo (que é quem ficou isolado) e com vértice em . Ele é desenhado assim:
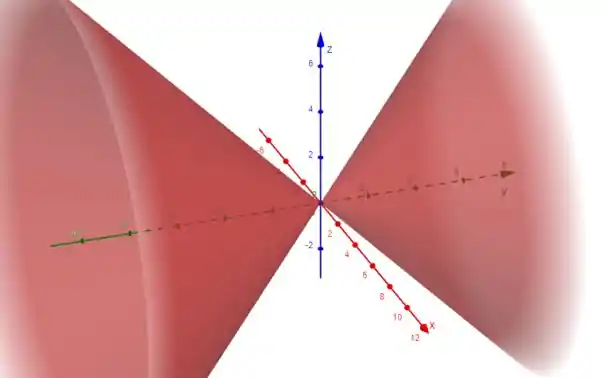
Passo 4
Por fim, para temos
Colocando dos dois lados:
Uma equação do tipo representa um hiperboloide de duas folhas ao longo do eixo . Então vamos escrever a equação dividindo tudo por :
Os vértices do hiperboloide vão estar em . Então essa superfície fica assim:
Sucesso entãooo, arrasamos!
Resposta
Para : indefinida
Para :
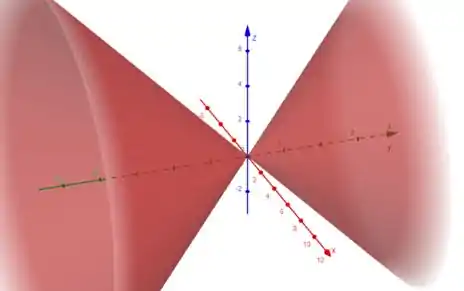
Para :
