Beleza, mas ainda precisamos saber quais são os possíveis valores que pode assumir, pra poder fazer ele variar nesses valores e, assim, obtermos todas as nossas curvas de nível, ou seja, o conjunto de nível da nossa função.

Vamos começar determinando todos os valores que pode assumir pra podermos encontrar nossos conjuntos de nível.

Temos

Isso não tem restrição nenhuma, né? Então significa que nosso pode assumir qualquer valor.

Então

Agora vamos fazer o variar dentro desse intervalo para saber todos os conjuntos de nível da nossa função.

Se :

Ou seja, temos um paraboloide elíptico com eixo no eixo e bem certinho com a “bunda” na origem rsrs

Assim óh:

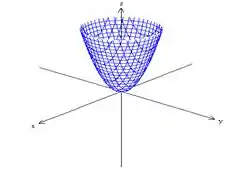
Agora, se fizermos o variar para além do zero, tanto positivamente quanto negativamente, o que acontece é que vamos estar deslocando o nosso paraboloide ao longo do eixo dele, que no caso é o eixo .

Assim, se a gente desloca nosso paraboloide de unidades para cima, no eixo e se , a gente desloca nosso paraboloide de unidades para baixo no eixo .

Easy game?

Juntando tudo, a representação geométrica de todos os conjuntos de nível que podemos ter é