2.1. Em cada caso, esboce a superfície de nível da função :
d. .
Passo 1
Fala aí! Tudo certinho? Esta questão está um pouco complicada? Relaxa que vamos tentar te ajudar. 😎

Nesse problema, queremos esboçar a superfície de nível da função em .
Tem alguma ideia de como fazer isso? 😁
Para esboçar uma superfície de nível de uma função , temos que igualar a onde representa o nível que vamos obter.
Dessa maneira, eliminamos uma dimensão da função e assim é possível esboçar a superfície formada no espaço tridimensional.
Sacou? Bora começar! 😉
Passo 2
Igualando a temos
Estamos interessados na superfície do nível , ou seja
Nesse caso, perceba que para , vamos ter circunferências paralelas ao plano com raio .
Esboçando essa superfície no espaço, vamos obter
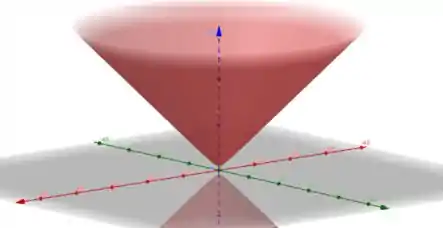
Fim! Iae, o que achou? Responde Aí! 😁