(Capítulo 14.1 – Exercício 66) Descreva as superfícies de nível da função.
Passo 1
E aí galerinha, tudo beleza? Bora lá resolver mais uma questão?

O objetivo dessa questãozinha aqui, é descrever as superfícies de nível da função dada. Tá, mas por onde começar? Como fazemos isso?
Essas superfícies de nível, servem para descrevermos funções com 3 variáveis, que é o caso da nossa função dada no enunciado. Elas mostram pra gente o comportamento da função, e pra calculá-las, basta igualarmos a uma função constante !
Em termos de quação vamos ter: .
Bora lá então!
Passo 2
Igualando a função dada, à função constante, temos que:
Se , não existem superfícies de nível. Então, vamos começar igualando a função a e partir disso. Vale lembrar aqui, que quando fizermos , teremos: . Essa coordenada será a origem!
Já quando , as superfícies de nível são elipsoides. Lembrando que elipses apresentam a seguinte equação característica:
Então, fazendo isso para a nossa equação, temos que:
A superfície de nível pode ser descrita pela equação acima! Para determinarmos as superfícies e termos algo como a imagem abaixo, basta determinarmos diferentes valores para e irmos colocando no gráfico.
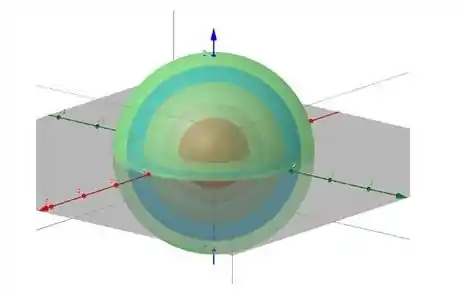
Pra essa questão é isso, pessoal!! Bora resolver mais uma?