Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Superfícies de Nível

Ver Teoria
Exercício 123456789101112131415161718192021222324252627282930313233

Enunciado

Descreva e esboce as superfícies de nível de f x , y , z = x 2 + y 2 - z 2 .

Passo 1

Para encontrar as superfícies de nível basta igualar a função a uma constante:

f x , y , z = k

⇒ x 2 + y 2 - z 2 = k

Note que, para identificar essa superfície, temos que analisar o sinal da constante k para cada caso: k > 0 , k < 0 e k = 0 .

Passo 2

Se k > 0 :

Podemos dividir os dois lados por k :

x 2 k + y 2 k - z 2 k = 1

Como k > 0 , podemos dizer que k = a 2 , onde a > 0 .

x 2 a 2 + y 2 a 2 - z 2 a 2 = 1

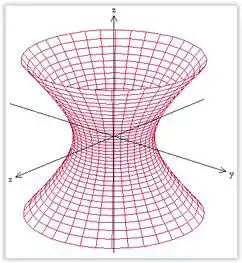
Esta superfície é um hiperboloide de uma folha, com eixo em z .

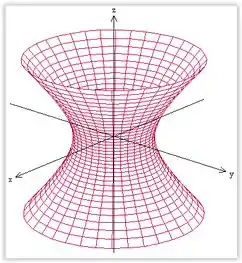
Passo 3

Se k = 0 :

Substituindo na equação:

x 2 + y 2 - z 2 = k

Temos que

x 2 + y 2 - z 2 = 0

⇒ z 2 = x 2 + y 2

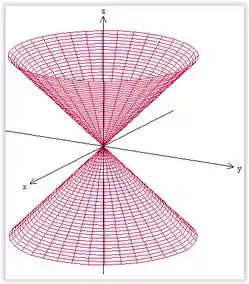
Esta superfície é um cone circular, com eixo em z .

- ''

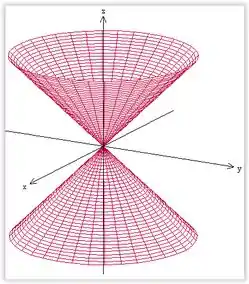
Passo 4

Se k < 0 :

Podemos dividir os dois lados por k :

x 2 k + y 2 k - z 2 k = 1

Como k < 0 , podemos dizer que k = - a 2 , onde a > 0 .

- x 2 a 2 - y 2 a 2 + z 2 a 2 = 1

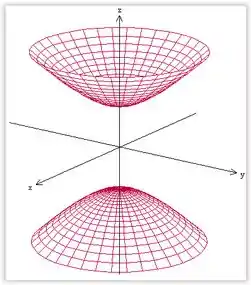
Esta superfície é um hiperboloide de duas folhas, com eixo em z .

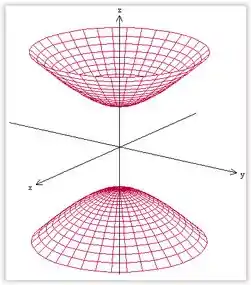
Resposta

x 2 + y 2 - z 2 = k

Se k > 0 : hiperboloide de uma folha

Se k = 0 : cone circular

Se k < 0 : hiperboloide de duas folhas

Exercícios de Livros Relacionados

Calcule, caso exista.d) underset((x , y) - (0,0))(l i m) (x y)/(x^2 + y^2)
Calcule underset((h , k) - (0,0))(l i m) ((f (x + h , y + k) - f (x , y) - 2 x h - k))/(‖(h , k)‖) , onde f (x , y) = x^2 + y^2
1 - Calcule caso existae ) underset((x , y) - (0 , 0))(lim) (x y (x - y))/(x^4 + y^4)
Calcule, caso exista.b) underset((x , y) - (0,0))(l i m) (x)/(sqrt(x^2 + y^2))
Represente graficamente e o domínio da função z = f x , y dada por b) f x , y = 1 - z