Água escoa em regime permanente no Venturi da figura. No trecho considerado, supõem-se as perdas por atrito desprezíveis e as propriedades uniformes nas seções. A área (1) é , enquanto a da garganta (2) é . Um manômetro, cujo fluido manométrico é mercúrio, é ligado entre as seções (1) e (2) e indica o desnível mostrado na figura. Pede-se a vazão da água que escoa pelo Venturi.
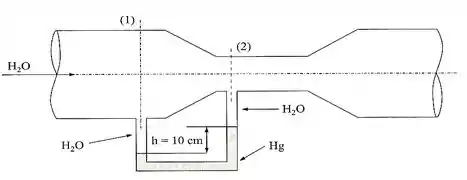
Considere
Passo 1
Queremos encontrar a vazão:
Para isso, precisamos da área e velocidade na seção (1) ou na seção (2).
Perceba que temos e .
Pela equação da continuidade, podemos relacionar e :
Passo 2
Substituindo valores:
Observe que não podemos determinar os valores de e , mas podemos relacioná-los.
Então, vamos aplicar a equação de Bernoulli entre os pontos (1) e (2).
Passo 3
Aplicando a equação de Bernoulli entre os pontos (1) e (2):
Se liga: Nesse caso, estamos aplicando a equação de Bernoulli em dois pontos do mesmo fluido.
Por isso temos uma mesma densidade nos dois lados da igualdade. É bom ficar atento pois, como existe outro fluido na questão, você pode acabar se confundindo.
Passo 4
Hipótese: como o escoamento é horizontal, desconsideramos diferença de alturas:
Logo:
Passo 5
Rearranjando:
Vamos lembrar que e estão relacionadas pela equação da continuidade:
Passo 6
Substituindo:
Passo 7
Isolando :
Agora, note que não conhecemos ainda .
Para isso, aplicamos o Princípio de Stevin no manômetro em “U”.
Passo 8
Aplicando Princípio de Stevin nos pontos (A) e (B):
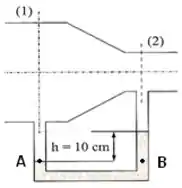
onde é a densidade do mercúrio e é a altura da coluna de mercúrio.
Pela figura:
Agora é só substituir os valores para determinar .
Passo 9
Substituindo valores:
Passo 10
Substituindo na equação anterior, para encontrar :
Passo 11
Agora podemos substituir para encontrar a vazão: