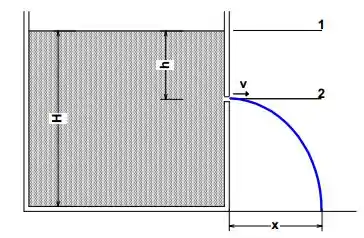
Um tanque contém água até uma altura . É feito um pequeno orifício na sua parede à profundidade da superfície, conforme a figura.
Mostre que a distância da base da parede até onde o jato atinge o solo é dada por .
Calcule a profundidade do buraco para que o jato emergente atinja o solo a uma distância máxima da base do tanque.
Passo 1
Primeiramente: Vamos analisar o problema sob a ótica da equação de Bernoulli, comparando o nível 1 ao nível 2 do fluído (conforme a figura). Dessa forma, vamos conseguir obter a velocidade do fluido no nível 2, o que permitirá resolver o resto da questão. Vamos obter as informações necessárias de cada nível:
Nível 1:
Altura da coluna de líquido: (a superfície é estática)
Nível2:
Altura da coluna de líquido:
Vamos equacionar agora:
Como , podemos cortar as pressões em ambos os lados da equação. Nesse ponto, a gente costuma ficar em dúvida sobre o por quê da pressão no ponto 2 ser a pressão atmosférica, e não a pressão hidrostática causada pela coluna de líquido de altura ....
Bom, a resposta é simples: Estamos considerando um ponto que está na iminência de sair do tanque e não exatamente dentro do tanque! Ou seja, é como se estivéssemos analisando um ponto que já está fora do tanque e, por isso, sujeito a pressão atmosférica do lado de fora!
Continuando...
Com esse valor, agora vamos poder resolver os itens e (:
Passo 2
Nos passos seguintes, nós vamos usar conceitos de cinemática. O movimento do fluído após sair pelo orifício, no nível 2, é obliquo. Bom, a velocidade é puramente horizontal, já que o fluido é expelido perpendicularmente à parede do tanque! Logo, a distância pode ser expressa por:
(eq.1)
No qual é o tempo de queda do fluido.
Bom, como a altura que as partículas do fluido vão percorrer é (olhe a figura),e o movimento na vertical em um lançamento obliquo é um ,é possível escrever:
Isolando
Substituindo o valor de e na eq.1:
Pronto, essa demonstração é a solução da (:
Passo 3
Vamos para a letra
Precisamos achar uma altura tal que a distância seja máxima. Bem, utilizaremos aquele velho conceito de máximos e mínimos de funções de uma variável de cálculo. Podemos considerar a relação encontrada anteriormente de , ou seja, uma função de
No entanto, é fácil perceber que essa função terá um máximo quando a expressão tiver um máximo. Fazendo , vamos encontrar o máximo dessa função, que é do segundo grau. Derivando em relação a :
Igualando a zero:
Pronto, essa é a resposta da letra (: