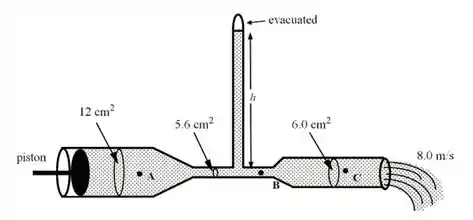
Um tubo de vidro tem três secções com áreas diferentes, cujos valores estão indicados na figura abaixo. Um pistão exerce uma força no lado esquerdo do tubo que faz o mercúrio dentro do tubo fluir, saindo do lado direito a uma velocidade de . Três pontos dentro do tubo estão indicados pelas letras A, e . Note que não é desenhado na escala correta e a densidade do mercúrio é Qual a pressão total no ponto ?
Passo 1
Vamos considerar o mercúrio um fluido ideal e que o fluxo não é turbulento. Assim podemos usar a equação da continuidade e Bernoulli.
Devido aos Pontos e estarem na mesma altura, podemos aplicar a equação de Bernoulli, que relaciona as propriedades de um fluido ideal ao longo de uma linha de corrente:
Podemos ainda considerar que , pela proximidade que este está da extremidade onde há a ssim:
Passo 2
Usando a equação da continuidade no ponto e no ponto temos:
Logo, substituindo a equação acima na equação de Bernoulli:
Passo 3
Substituindo os termos do enunciado na equação final do Passo 2, temos:
Resposta
Letra C.