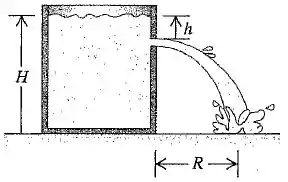
A água de uma grande tanque aberto com paredes verticais possui uma profundidade ( figura abaixo). Um orifício é aberto na parede vertical a uma profundidade abaixo da superfície da água.
- Qual é a distância entre a base do tanque e o ponto onde a corrente atinge o solo?
- Qual a distância acima da base do tanque devemos fazer um segundo furo para que a corrente que emerge dele tenha um alcance que igual ao do primeiro furo?
Passo 1
a)
Bom, o que você precisa fazer primeiro aqui?
Você precisa, primeiro, calcular a velocidade do esguicho de água. Como a gente viu na teoria, vamos tomar o ponto na superfície da água e ponto na saída do jato.
Passo 2
Assim:
Beleza. Agora precisamos achar a distância horizontal que esse jato percorre antes de atingir o solo.
Pra issoo, vamos ter que primeiro achar o tempo de queda.
Esse jato cai da seguinte altura:
Como a velocidade vertical inicial é nula, podemos usar a fórmula:
A distância horizontal percorrida vai ser esse tempo vezes a velocidade achada:
Passo 3
b)
Agora nós vamos pegar uma distância em relação à base do tanque. Vamos chamá-la de
Como a medida vai ser a altura do jato, o tempo de queda livre vai ser dado por:
Como nós fizemos no caso anterior.
Já a altura em relação à superfície vai ser dada por:
Assim, a velocidade do jato vai ser:
Assim, a distância horizontal será:
Fazendo
Comparando, percebemos que:
Ou seja, pra se ter a mesma distância, basta pegar a mesma altura , só que agora sendo medida a partir da base.
Resposta
a)
b)