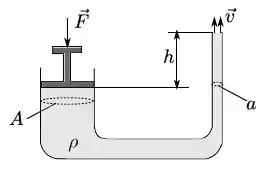
Um chafariz é feito usando-se um tubo em preenchido com um líquido de densidade , conforme figura. Do lado esquerdo a área da seção transversal do tubo é e do lado direito a área da seção transversal do tubo é . A saída do chafariz, do lado direito, está a uma altura do êmbolo e tem área igual ao tubo. Suponha que e que a pressão atmosférica seja . Qual o valor da força externaque se deve aplicar sobre o êmbolo para que o líquido saia do chafariz com uma velocidade
?
Passo 1
Para resolver esse tipo de questão, vamos definir os pontos 1 e 2, como mostrado na figura abaixo e lembrar lá do principio de Pascal e da Equação de Bernoulli.
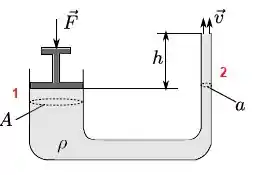
Ou seja, o ponto 1 é onde está sendo aplicada a força F. O ponto 2 é o bocal de saída, com velocidade .
A Equação de Bernoulli é:
A pressão no ponto 1 vai ser:
E, pelo Princípio da Continuidade, podemos escrever:
Mas como , . Então:
Beleza. Agora eu vou considerar a altura do êmbolo ao qual está sendo aplicada a força como referencial. De forma que e . Então:
Isolando :
Mas como a saída do bocal, no ponto 2, está na atmosfera, . Então:
Isolando :
Resposta
Letra A.