O ar flui através do tubo da figura abaixo com uma vazão de . Suponha que o ar seja um fluido ideal com densidade de enquanto mercúrio apresenta densidade de .
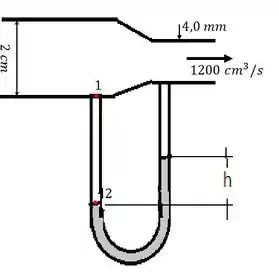
Desenhe as linhas de fluxo na figura.
A pressão no ponto é maior, igual ou menor que no ponto ? E em pontos correspondentes de mesma altura no ramo do lado direito? Justifique.
Qual é a altura de mercúrio no ramo direito do tubo em Se usar a equação de Bernoulli, deixe explicito em que pontos você a está aplicando.
Passo 1
As linhas de fluxo não se cruzam e são mais espaçadas onde a área é maior e menos espaçada onde a área é menor. Por isso o desenho deve ser algo assim:
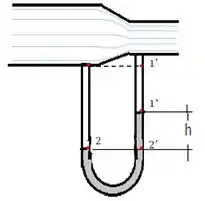
Passo 2
Os pontos e estão imersos no mesmo fluido, o ar. Então o podemos usar o principio de Stevin e o conceito de pressão hidrostática para nos ajudar a descobrir a pressão em cada ponto.
Como os pontos estão na no mesmo fluido e na mesma vertical. Então a pressão em será a pressão em acrescido da pressão causada pela coluna de ar.
A questão é que como a densidade do ar é muito pequena e a coluna de ar também é pequena então a pressão causada por essa coluna de ar será mínima, podendo ser desprezada.
Vamos calcula-la para comprovar isso.
A pressão devido à coluna de ar é:
As pressões são dadas geralmente na ordem de , então vemos essa pressão que encontramos é nada perto de . Por isso podemos dizer que:
Passo 3
Agora os pontos correspondentes no lado direito.
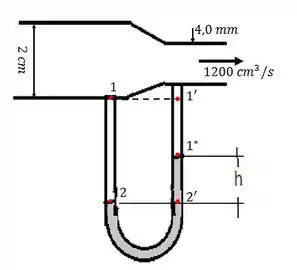
Bem Terminamos de ver que a pressão causada por uma pequena coluna de ar pode ser desconsiderada e por isso a pressão em é igual a pressão em .
Já a pressão em será a pressão em acrescida da pressão causada pela coluna de mercúrio. Como a densidade de mercúrio é alta . Essa pressão não pode ser desconsiderada. E por isso:
Assim,
Passo 4
Em um tubo em a diferença de altura entre cada lado é causada pela diferença de pressão de cada lado. Por isso a primeira coisa que temos que fazer é descobrir o valor da pressão em cada lado.
Na questão temos a vazão do fluido, área da seção dos canos e queremos a pressão. Então pelo principio da continuidade a vazão não varia e conseguimos relacionar as áreas das seções com as velocidades do fluido. E depois com a equação de Bernoulli conseguimos relacionar as velocidades com as pressões em e .
Bem, vamos juntar as informações que o enunciado nos forneceu. Ele nos deu os diâmetros de cada tubo. E a vazão de saída. Então precisamos descobrir as velocidades do fluido em cada tubo .
Para isso vamos usar o principio da continuidade que diz que por conservação de massa sabemos que a vazão não vai mudar.
A vazão é o que equivale. A área no tubo é e no tubo é
Então a velocidade em cada tubo será:
Vamos passar essa velocidade para :
Passo 5
Agora que temos a velocidade em e em . Podemos usar a equação de Bernoulli para descobrir a relação entre as pressões.
A equação será aplicada ao ponto central no tubo acima do ponto , chamaremos essa ponto de também. E ao ponto central do tubo menor acima do ponto e por isso chamaremos esse ponto de .
Como os pontos centrais dos tubos estão na mesma altura . Então esse termo se cancela.
Reescrevendo a equação acima deixando as pressões em um lado, temos:
Substituindo os valores da densidade do ar e das velocidade descobrimos que a diferença de pressão entre os pontos é:
Lembre-se que a velocidade deve estar em , por isso multiplicamos a equação por .
Como vimos no inicio a diferença de altura é causada pela diferença de pressão entre os lados. Isso quer dizer que a pressão causada pela coluna de líquido é igual a diferença de pressão em cada lado do tubo.
Resposta
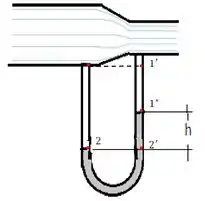
e