Na figura está representado um grande reservatório de água de altura , com uma tubulação horizontal de raio acoplada na lateral . Esta tubulação muda para uma tubulação vertical de menor raio na saída 2, , onde a água escoa para a atmosfera. Na figura
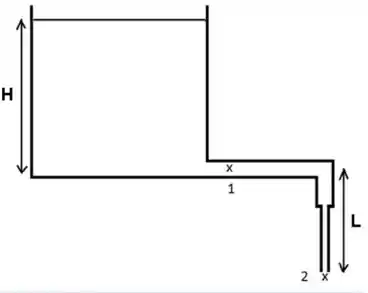
- Determine a altura para que a velocidade na saída 2da tubulação seja de
- Calcule a diferença de pressão entre as saídas 1 e 2 da figura, .(Valem os valores do item a).
- Quando a água escoa pra atmosfera no ponto 2, observa-se que o diâmetro do filete de água diminui enquanto cai. Calcule a distância que a água deve cai pra que o raio diminuía de ( na saída 2) para .( Valem os valores do item a).
Passo 1
a):
Vamos aplicar Bernoulli entre o ponto mais alto do reservatório e entre o ponto onde a água escoa:
No ponto mais alto do reservatório, a velocidade é nula. Além disso, vamos considerar a altura como a altura mais baixa de todas, a altura do cano que libera água pra atmosfera.
Além disso:
:
Passo 2
b):
Vamos primeiro aplicar a equação da continuidade entre o ponto final onde a água desce e o ponto onde tem um , na figura. Isso é:
A área é dada por:
E a área é dada por:
Então:
Bernoulli entre os pontos 1 e 2:
Passo 3
c):
Vamos usar a equação da continuidade entre 1 e 2, sendo 1 o ponto inicial( onde o raio é, e 2 é onde o raio tem
Agora vamos aplicar Bernoulli entre esses dois pontos:
Lembrando que . Então:
Resposta
a):
b):
c):