Um orifício de de diâmetro encontrase abaixo da superfície do tanque de água de de diâmetro. Qual a vazão de volume através do orifício, em ?
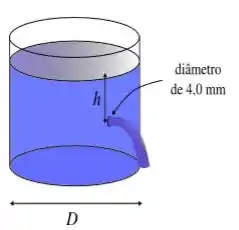
Passo 1
Essa é aquela questão típica onde vamos usar a equação de Bernoulli, e o princípio da continuidade para resolve-la.
Então vamos lá, temos dois estados a partícula de água na superfície do tanque sofrendo a pressão atmosférica apenas, com uma altura que vamos adotar como zero, e velocidade zero, pois a área do tanque é muito maior que a do orifício.
Já o segundo estado é a partícula que está no orifício, ela também sofre a ação da pressão da atmosfera, está a uma altura de abaixo do ponto que adotamos como , por isso é negativa e tem uma velocidade , desconhecida ainda, então
Isolando a velocidade, chegamos em
Passo 2
Beleza, descobrimos a velocidade com que a água escapa, mas queremos a vazão que é
O enunciado nos forneceu o diâmetro do furo, assim conseguimos calcular a área dele
Voltando a equação da vazão temos
Descobrimos a vazão em , mas queremos ela em
Então devemos lembrar que
E
Então vamos ter que
Resposta
Alternativa