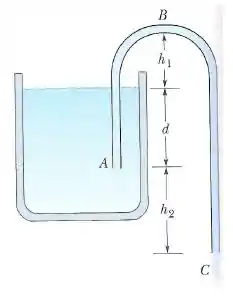
A figura mostra um sifão, que é um tubo usado para transferir líquidos de um recipiente para outro. O tubo deve estar inicialmente cheio, e se esta condição é satisfeita o líquido escoa pelo tubo até que a superfície do líquido no recipiente esteja no mesmo nível que a extremidade . O líquido tem densidade igual a e viscosidade desprezível. As distâncias mostradas na figura são , e . Considere .

1. Com que velocidade o líquido sai do tubo no ponto ?
2. Se a pressão atmosférica é , qual é a pressão do líquido no ponto , o ponto mais alto do tubo?
3. Qual é o máximo valor de , mantidos e , para que o líquido continue escoando?

a):

Bom galera, vamos considerar que o nível de altura nula passa pelo ponto c. Dessa forma, o ponto c tem altura igual a zero.

Vamos agora aplicar Bernoulli entre e o ponto logo acima de na superfície do fluido(Vamos chamá-lo de :

Vamos às características de cada ponto:

A altura de do ponto foi medido em relação ao nível de altura nula, por isso esse valor. O valor da velocidade do fluido em tende a zero, já que o fluido começa a subir o tubo ali, e, somente a partir dali ele começa a ganhar velocidade.

Mas por que o valor da pressão de é igual ao valor da pressão atmosférica?

Porque, como a velocidade ali é nula, estamos no regime da hidrostática. Ou seja...,podemos aplicar Stevin!

Isso quer dizer que o valor da pressão de é igual ao valor da pressão do ponto do fluido logo ao lado, fora do cano, já que ambos possuem a mesma altura. E o valor da pressão na superfície do fluido é

O que queremos saber.

Bem, a altura é zero pois o referencial de altura nula está passando por . A pressão é a pressão atmosférica pois o cano está aberto pra atmosfera.

Por Bernoulli: