UFRJ – Física 2 2020.2 – P1 – Questão 6
Um reservatório A com superfície fechada, é conectado a um tubo B, aberto para a atmosfera, com área de seção reta constante e muito menor que a superfície de água em A, como mostra a figura.
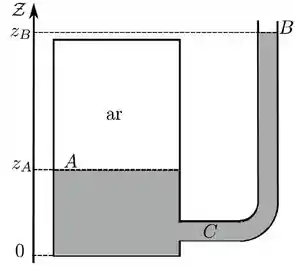
Considerando que existe um fluxo de água entre esses dois reservatórios, a velocidade da água no ponto C, indicado na figura, é dada por:
Escolha uma:
Passo 1
Fala pessoal, tudo bem? Vamos começar?
Aqui, temos um fluxo de água entre os reservatórios, ou seja: um problema de hidrodinâmica, já que temos o fluido em movimento. Beleza?
Bom, nós temos todas as informações necessárias para aplicar Bernoulli nos pontos e , certo? Então bora fazer isso! A equação fica assim:
Beleza, aqui, temos que levar em conta duas coisas: a primeira é que, como a superfície em é muuuito maior que em , nós podemos desconsiderar a velocidade do fluido em . Isso porque . Em comparação com é como se o fluido em não se mexesse, beleza? E vamos botar por isso.
Próximo ponto é que a velocidade em será a mesma velocidade em , certo?? Podemos provar isso pelo princípio da continuidade, pois sabemos que e temos que e , logo . Tranquilo?
Temos, também, que . Então, vamos colocar tudo sendo . Ok?
Passo 2
Então, nossa equação de Bernoulli fica assim agora:
Agora, vamos isolar :
Passar o multiplicando:
O dividindo e colocar o em evidência no segundo termo:
Agora, é só tirar a raiz quadrada desse cara aí e chegar na resposta:
Com isso, vemos que a opção correta é a (b). Tranquilo?? 😊
Espero ter ajudado!