O tubo horizontal mostrado na figura apresenta seção reta com área igual a em sua parte mais larga e em sua constrição. A água flui no tubo, e vazão volumétrica é igual a (, Calcule:
- A velocidade do escoamento na parte mais larga e na constrição.
- A diferença de pressão entre essas duas partes.
- A diferença de altura entre os dois níveis de mercúrio existente no tubo em U.
Dado:
Passo 1
a)
Bom, como temos o valor da vazão, fica fácil calcular a velocidade em cada uma das áreas. Isso por causa do princípio da continuidade. Esse princípio nos diz que a vazão é constante. Então basta a gente usar a fórmula:
Na parte larga:
Se liga: Ali
E na constrição:
Viu como a velocidade aumenta quando a área transversal diminui? Isso acontece porque a vazão é constante (princípio da continuidade) =D
Passo 2
b)
Como o escoamento é horizontal podemos afirmar que: . Então, aplicando Bernoulli nos dois pontos (parte larga e constrição), vamos ter:
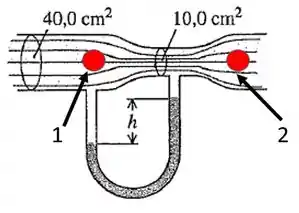
Galera, o problema pediu a diferença de pressão, por isso vamos isolar o termo como um todo.
Passo 3
c)
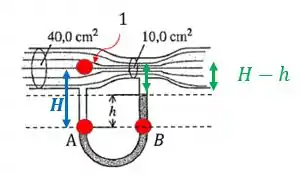
Pra calcular essa diferença vamos usar o os pontos A e B dessa figura acima! Nós vamos fazer porque o líquido no tubo em está parado e, portanto, podemos utilizar o princípio de Stevin:
A pressão no ponto A vai ser a pressão do ponto somada com a pressão feita pela coluna de água de altura
Já a pressão no ponto B vai ser a pressão no ponto B somada com as pressões das coluna de água (com altura ) e da coluna de mercúrio (com altura )
Passo 4
Igualando as pressões A e B
Expandindo esse termo com a densidade da água na direita podemos ver que vai cortar o termo
Agora basta isolar
Já calculamos no passo 2! Então agora é só substituir os valores e correr pro abraço!
Resposta
a)
b)
c)