Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Aplicações da Hidrodinâmica

Ver Teoria
Exercício 261234567891011121314151617181920212223242527282930313233343536373839404142434445464748

Enunciado

Um tanque de água encontra-se sobre um carrinho que pode mover-se sobre um trilho horizontal com atrito desprezível. Há um pequeno orifício numa parede a uma profundidade h   =   45   c m abaixo do nível da água no tanque. A aérea do orifício é A   =   2   c m 2 , a massa inicial da água é M 0   =   30   k g e a massa do carinho e do tanque é m 0   =   10   k g . Considerar g   =   10   m / s 2 . A densidade da água é ρ = 10 3   k g / m 3 .

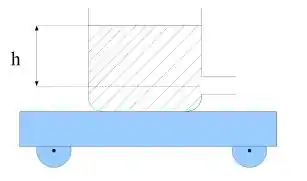
a) Qual é a velocidade inicial v 0 da água saindo do tanque?

b) Qual é a vazão R da água na saída do tanque?

c) No tempo inicial, a velocidade do carrinho é nula. Durante um intervalo de tempo ∆ t , uma massa ∆ m de água é ejetada. Qual é a variação de velocidade do carrinho durante ∆ t ? Escrever o resultado em função de R ,   ρ , m o ,   M o ,   ∆ t e da velocidade relativa da água ejetada em relação ao carrinho.

d) Qual é o valor da aceleração inicial do carrinho?

Passo 1

A) Pela equação de Bernoulli

z 1 + v 1 2 2 g + P 1 ρ g = z 2 + v 2 2 2 g + P 2 ρ g

z 2 - z 1 + v 1 2 2 g + P A T M ρ g = v 0 2 2 g + P A T M ρ g

v o = 2 g h = 3 m / s

Passo 2

B)

R = A × v o

R = 2 × 10 - 4 × 3 = 6 × 10 - 4 m 3 / s  

Passo 3

C)

∆ m = R × ∆ t × ρ

∆ v = v f - v i = v á g u a   e j e t a d a × ln ⁡ m i m f

Mas

m i m f = 1 + ∆ m m f = M o + m o M o + m o - R ∆ t ρ

Passo 4

D)

m × d v d t = d m d t × v r e l

Onde d m d t é a vazão mássica

d m d t = R × ρ

Então, a aceleração do carinho

a = R × ρ × 1 m × v o

a = R ρ v o M o + m o = 6 × 10 - 4 × 10 3 × 3 40

a = 4,5 × 10 - 2 m / s  

Resposta

A) 3 m / s

B) 6 × 10 - 4 m 3 / s

C) M o + m o M o + m o - R ∆ t ρ

D) 4,5 × 10 - 2 m / s

Exercícios de Livros Relacionados

A figura mostra um sifão, que é um tubo usado para transferir líquidos de um recipiente para outro. O tubo A B C deve estar inicialmente cheio, mas, se essa condição é satisfeita, o líquido escoa pelo
Uma transição abrupta ocorre nos números de Reynolds de cerca de 3 * 10 5 , onde o arrasto em uma esfera se move através de um fluido diminui abruptamente. Estimar a velocidade com que essa transição
O cano de saída do esgoto de uma casa construída em uma encosta está a 6,59m abaixo do nível da rua. Se o cano coletor do esgoto está 2,16m abaixo do nível da rua, calcule a menor diferença de pressão
Qual é a área mínima (em metros quadrados) da supefície superior de uma placa retangular de gelo com 0,441m de espessura que flutua na água doce para que seja capaz de sustentar um automóvel de 938k g
A água flui através de um tubo horizontal de 25,0 cm de comprimento um diâmetro interno de 1,20 mm em 0,300 mL/s. Encontre a diferença de pressão necessária para conduzir esse fluxo se a viscosidade d