Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Aplicações da Hidrodinâmica

Ver Teoria
Exercício 171234567891011121314151618192021222324252627282930313233343536373839404142434445464748

Enunciado

UFF – Física III – P1 – 2022.1 – Q7

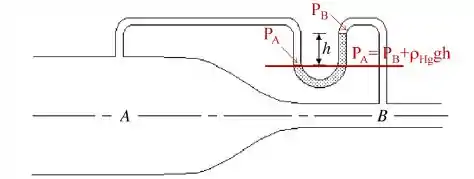
Água escorre por um cano horizontal de calibre variável, como mostrado na Figura. No ponto A, a área de secção transversal é de 25,0 cm² e a velocidade da água é de 2,00 m/s. Em B, a área é de 16,0 cm². O fluido no manômetro é mercúrio cuja desidade é de 13,6 × 10 3 kg/m³. Trate a água como fluido ideal com densidade de 1000 kg/m³. Despreze a variação da pressão ao longo da seção transversal do cano. Qual é a leitura h do manômetro?

  1. 0,546 cm
  2. 1,31 cm
  3. 2,81 cm
  4. 2,12 cm
  5. 3,36 cm

Passo 1

E aí, galerinha! Tudo na paz por aí?

Olha que maravilha de questão, hein! Porque aqui a gente vai precisar lembrar de dois conceitos e equações importantíssimas da hidrostática e hidrodinâmica. Você se lembra qual é a equação super mega importante da hidrostática?

P = ρ g h

Bem, A gente quer saber qual é a leitura h no manômetro, certo?

Se olharmos pro desenho da linha feita, temos que:

P A = P B + ρ H g g h

h = P A - P B ρ H g g

Opa, temos uma equação aí que nos dará exatamente o valor da altura h , mas DE ONDE a gente vai tirar essa diferença de pressão aí PA – PB?

Da hidrodinâmica temos a nossa lindona da equação de Bernoulli ideal:

P A ρ g + V A 2 2 + z A = P B ρ g + V B 2 2 + z B

Onde as pressão do ponto A e B são dadas pelas variáveis P A e P B , respectivamente e as velocidades A e B também são dadas por VA e VB, respectivamente. As alturas dos pontos A e B são dadas pela letrinha z.

Já captou a ideia do que precisamos fazer, né? Senão ainda, relaxa e vem comigo !!!

Passo 2

Note que da equação de Bernoulli a gente consegue isolar P A - P B

P A ρ g + V A 2 2 + z A = P B ρ g + V B 2 2 + z B

P A - P B ρ g = V B 2 - V A 2 2 + z B - z A

Note que essas alturas z A e z B são iguais, pois estamos pegando o mesmo ponto (em azul no desenho abaixo).

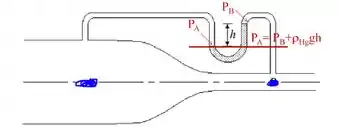
Logo, podemos escrever que:

P A - P B = ρ g V B 2 - V A 2 2

ATENÇÃO: A densidade que tá aqui é da água e não do mercúrio, beleza?

Tá, mas a gente não tem a velocidade V B , né? Aquela dada no enunicado é na secção A ☹

E agora? O que fazer? Você tem ideia?

Passo 3

No balanço de massa em regime estacionário e sem reação química, a gente diz que:

“A massa que entra é igual a massa que sai”

Isso serve também pra vazão mássica ou volumétrica, em outras palavras, a propriedade que entra tem que ser igual a que sai. Podemos então dizer que a vazão volumétrica que entra na secção A é a mesma que sai na secção B.

E como calculamos vazão volumétrica?

Q = V A

Ou seja, a vazão volumétrica é o produto da velocidade pela área de secção transervsal. Com isso, podemos dizer que:

Q A = Q B

V A A A = V B A B

V B = V A A A A B

Lembrando que temos que passar as variáveis para o SI, ou seja, A 1 = 25   c m 2 = 0,0025   m ² e A B = 16   c m 2 = 0,0016   m ² .

Passo 4

Substituindo na equação de P A - P B

P A - P B = ρ g V A A A A B 2 - V A 2 2

Podemos agora substituir esse trombolho dentro da equação de h que vimos lá no passo 1!

h = P A - P B ρ H g g

h = ρ g V A A A A B 2 - V A 2 2 ρ H g g

h = ρ V A A A A B 2 - V A 2 2 ρ H g

h = 1000 2 × 0,0025 0,0016 2 - 2 2 2 × 13,6 × 10 3 = 0,0212   m

h = 2,12   c m

See you na próxima questão heinnn!!

Resposta

(D)

Exercícios de Livros Relacionados

A figura mostra um sifão, que é um tubo usado para transferir líquidos de um recipiente para outro. O tubo A B C deve estar inicialmente cheio, mas, se essa condição é satisfeita, o líquido escoa pelo
Uma transição abrupta ocorre nos números de Reynolds de cerca de 3 * 10 5 , onde o arrasto em uma esfera se move através de um fluido diminui abruptamente. Estimar a velocidade com que essa transição
O cano de saída do esgoto de uma casa construída em uma encosta está a 6,59m abaixo do nível da rua. Se o cano coletor do esgoto está 2,16m abaixo do nível da rua, calcule a menor diferença de pressão
Qual é a área mínima (em metros quadrados) da supefície superior de uma placa retangular de gelo com 0,441m de espessura que flutua na água doce para que seja capaz de sustentar um automóvel de 938k g
A água flui através de um tubo horizontal de 25,0 cm de comprimento um diâmetro interno de 1,20 mm em 0,300 mL/s. Encontre a diferença de pressão necessária para conduzir esse fluxo se a viscosidade d