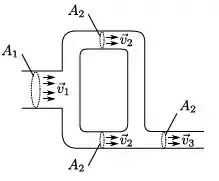
Consideremos um fluido incompressível realizando um escoamento estacionário como mostrado
na figura. Escreva a velocidade do fluido em função de e .
Passo 2
Aqui a primeira coisa que você tem que perceber é que é a área.
Pelo princípio da continuidade:
Repare que:
Trocando:
Passo 3
Vamos brincar com essas equações:
E agora a outra:
Substituindo :
Como pela figura:
Temos que:
Então:
Resposta
Letra A.
Exercícios de Livros Relacionados
A figura mostra um sifão, que é um tubo usado para transferir líquidos de um recipiente para outro. O tubo A B C deve estar inicialmente cheio, mas, se essa condição é satisfeita, o líquido escoa pelo
Uma transição abrupta ocorre nos números de Reynolds de cerca de 3 * 10 5 , onde o arrasto em uma esfera se move através de um fluido diminui abruptamente. Estimar a velocidade com que essa transição
O cano de saída do esgoto de uma casa construída em uma encosta está a 6,59m abaixo do nível da rua. Se o cano coletor do esgoto está 2,16m abaixo do nível da rua, calcule a menor diferença de pressão
Qual é a área mínima (em metros quadrados) da supefície superior de uma placa retangular de gelo com 0,441m de espessura que flutua na água doce para que seja capaz de sustentar um automóvel de 938k g
A água flui através de um tubo horizontal de 25,0 cm de comprimento um diâmetro interno de 1,20 mm em 0,300 mL/s. Encontre a diferença de pressão necessária para conduzir esse fluxo se a viscosidade d