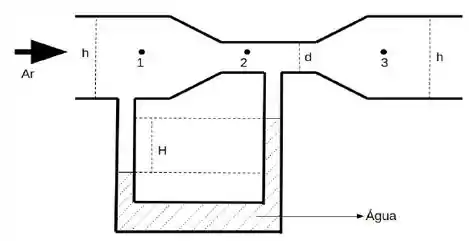
Sobre os pontos 1, 2 e 3 (à mesma altura) representados na figura, marque a única alternativa correta:
- As pressões nesses pontos são iguais, assim como as velocidades.
- As pressões nos pontos 1 e 3 são iguais entre si e menores que a pressão no ponto 2. As velocidades nos pontos 1 e 3 são iguais entre si e maiores que a velocidade no ponto 2.
- As pressões nos pontos 2 e 3 são iguais entre si e menores que a pressão no ponto 1. As velocidades nos pontos 2 e 3 são iguais entre si e maiores que a velocidade no ponto 1.
- As pressões nos pontos 1 e 3 são iguais entre si e maiores que a pressão no ponto 2. As velocidades nos pontos 1 e 3 são iguais entre si e menores que a velocidade no ponto 2.
- As pressões nos pontos 1 e 3 são iguais entre si e maiores que a pressão no ponto 2. As velocidades nos pontos 1 e 3 são iguais entre si e maiores que a velocidade no ponto 2.
Passo 1
Bom, antes de tudo, vamos lembrar de duas equações muito importantes, que é a equação do princípio da continuidade:
E a equação de Bernoulli:
Passo 2
Analisando a equação da continuidade, vemos que os pontos 1 e 3, têm o mesmo raio e , logo suas velocidades serão iguais. Já o ponto 2 tem raio menor, portanto sua velocidade de escoamento será maior que os pontos 1 e 3.
A pressão depende do fator h, ou seja, da altura da coluna de fluido que está sobre o ponto. Logo, a altura da coluna de fluido nos pontos 1 e 3 é menor que no ponto 2. Portanto, a pressão em 1 e 3 será maior que no ponto 2.
Resposta
Letra D
Exercícios de Livros Relacionados
A figura mostra um sifão, que é um tubo usado para transferir líquidos de um recipiente para outro. O tubo A B C deve estar inicialmente cheio, mas, se essa condição é satisfeita, o líquido escoa pelo
Uma transição abrupta ocorre nos números de Reynolds de cerca de 3 * 10 5 , onde o arrasto em uma esfera se move através de um fluido diminui abruptamente. Estimar a velocidade com que essa transição
O cano de saída do esgoto de uma casa construída em uma encosta está a 6,59m abaixo do nível da rua. Se o cano coletor do esgoto está 2,16m abaixo do nível da rua, calcule a menor diferença de pressão
Qual é a área mínima (em metros quadrados) da supefície superior de uma placa retangular de gelo com 0,441m de espessura que flutua na água doce para que seja capaz de sustentar um automóvel de 938k g
A água flui através de um tubo horizontal de 25,0 cm de comprimento um diâmetro interno de 1,20 mm em 0,300 mL/s. Encontre a diferença de pressão necessária para conduzir esse fluxo se a viscosidade d