Um tubo horizontal tem seção reta na parte mais larga e seção reta na parte mais estreita. O tubo possui um pistão que quando pressionado, aplica, ao atingir o regime estacionário, uma pressão e uma velocidade ao ar na parte larga do tubo. A parte estreita do tubo está conectada por um canudo vertical a um recipiente aberto contendo água. A distância vertical entre o tubo horizontal e a superfície livre da água é . Considere conhecidas as densidades do ar e da água , a aceleração da gravidade local e a pressão atmosférica . Faça a aproximação de que o ar seja incompressível.
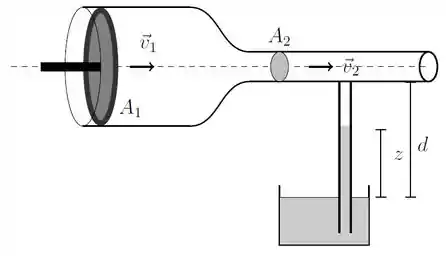
a) Determine a pressão na parte estreita em função da pressão e da velocidade na parte larga do tubo e da razão entre as seções retas.
b) Determine a altura da coluna de água no canudo vertical.
c) Determine a razão necessária para que a água seja aspirada através do canudo, entrando no tubo horizontal.
Passo 1
Letra : Primeiramente, vamos lembrar de duas equações: a equação de Bernoulli e a equação da continuidade.
Para falarmos da equação de Bernoulli, imagine a situação dada na imagem abaixo.
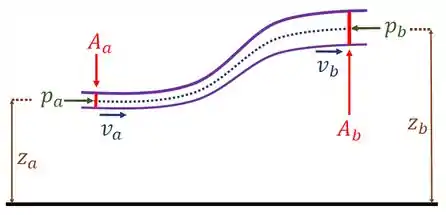
Na altura , o fluido possui uma pressão e uma velocidade . Na altura , o fluido possui uma pressão e uma velocidade . A equação de Bernoulli nos diz que todas essas quantidades se relacionam por
sendo a densidade do fluido (considerada constante) e a aceleração da gravidade.
Falaremos agora da equação da continuidade. Considere novamente a figura anterior.
No ponto onde a área da seção reta é a velocidade do fluido é . Já no ponto onde a área da seção reta é a velocidade do fluido é . Para fluidos incompressíveis (densidade constante), a equação da continuidade nos diz que
ou seja, se a área da seção reta diminui num ponto, a velocidade do fluido aumenta neste mesmo ponto, e vice-versa.
Isso pode ser visto quando lavamos a varanda de casa com uma mangueira. Ao apertamos a ponta da mangueira que sai água (diminuímos a área da seção reta, aumentamos a velocidade da água, e assim o seu alcance (a água vai mais longe).

Passo 2
Para determinar a pressão , aplicaremos a equação de Bernoulli em nosso tubo nos pontos cuja áreas da seção reta são e .
Como esses pontos estão sobre o eixo do tubo (que está na horizontal), então ambos os pontos estão a uma mesma altura do solo, isto é, . Não confunda com a altura do líquido dentro do canudo!!!Deste modo, temos que
Agora, vamos utilizar a equação da continuidade. Sabemos que nos pontos onde a seção reta possui áreas e , temos quePortanto,
Passo 3
Letra : Para determinar a altura do líquido dentro do canudo, utilizaremos a lei de Stevin. Considere a figura abaixo.
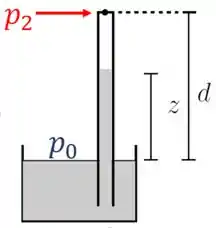
Na figura anterior, temos que no topo do canudo a pressão é , enquanto que na bacia de água (onde o canudo está mergulhado) a pressão é igual a atmosférica .
Assim, pela lei de Stevin, temos que
sendo a densidade do ar e a densidade da água.
Podemos escrever a equação anterior da seguinte forma
onde colocamos em evidência nos dois últimos termos. Veremos no próximo passo o porquê disso.
Passo 4
Poderíamos isolar o da equação anterior e resolver o item. No entanto, para facilitar nossa vida, faremos uma aproximação. Consideraremos que a densidade da água é muito maior que a densidade do ar , isto é,
Para uma pressão de e uma temperatura de , a densidade do ar é e da água é . Se pensarmos bem, essa consideração não é absurda, né?
Deste modo, quando olhamos a equação
vemos que o termo que multiplica pouco contribui na equação, pois . Deste modo, podemos desconsiderá-lo da equação e aproximar a mesma por
Assim, isolando , temos que
Passo 5
Letra : Mostramos no primeiro item que a pressão pode ser escrita como
Assim, se isolarmos , temos que
Ainda não terminamos!! Precisamos saber a pressão na qual a água é aspirada através do canudo entrando no tubo horizontal.
Para determinar essa pressão , podemos lembrar do item anterior. Mostramos que na aproximação de , a pressão satisfaz
Assim, quando a água é aspirada pelo canudo, significa que a altura da coluna de água é igual a distância (pois a água subiu até o tubo horizontal!). Logo,
Agora sabemos a pressão na qual a água é aspirada pelo canudo. Deste modo, substituindo na equação de , temos que