Dois tanques abertos estão cheios de um mesmo fluido de densidade constante, como ilustrado na figura. Um tubo horizontal tem uma extremidade conectada ao fundo do primeiro tanque e outra extremidade aberta, de modo que o fluido pode escoar para fora do tanque. O tubo possui um estrangulamento () onde a área da seção reta é a metade da área nas extremidades ( e ). Conectamos com um tubo em U o estrangulamento ao segundo tanque, de modo que a extremidade do tubo fica imersa no fluido. Com isso uma coluna de fluido preenche o tubo até uma a altura , após atingido o equilíbrio. Considere que a densidade do ar entre os pontos e é suficientemente pequena para desprezarmos variações de pressão com a altura. Considere também que as áreas das superfícies de fluido nos dois tanques são muito maiores que as das seções retas do tubo horizontal, que o escoamento do fluido através do mesmo é estacionário e que a aceleração da gravidade e a pressão atmosférica são constantes e conhecidas em todos os pontos da figura.
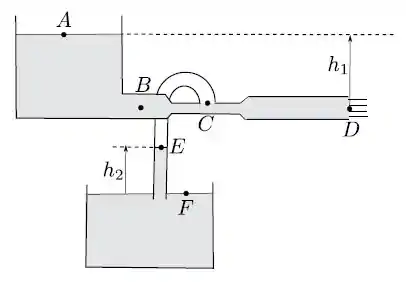
- Calcule a velocidade de escoamento do fluido no ponto indicado na figura.
- Calcule a velocidade do escoamento no ponto .
- Calcule a pressão manométrica (diferença entre a pressão absoluta e a pressão atmosférica) no ponto .
- Calcule a altura da coluna de fluido em termos da altura .
Passo 1
a)
Aqui a gente pode aplicar Bernoulli entre os pontos A e D. Lembrando que ,na superfície de um tanque com dimensões muito maiores que as dimensões dos encanamentos, podemos desprezar a velocidade do fluido.
Assim:
Vamos considerar como o nível zero de altura o nível do ponto D. Logo, tem altura zero e tem altura . Como ambos os pontos estão abertos pra atmosfera, a pressão dos dois é igual à pressão atmosférica, que vamos chamar de Logo:
Passo 2
b)
Se a gente sabe a velocidade no ponto e a relação entre as áreas das seções transversais no ponto e , a gente pode aplicar a equação da continuidade entre os pontos.
Então, como a vazão se conserva, temos:
Só que o enunciado nos diz que a área de é a metade da área de , logo:
Passo 3
c)
A gente pode escolher aplicar Bernoulli entre e ou entre e . Vamos escolher entre e
Aplicando:
Repare que não colocamos as energias das alturas porque são iguais ( mesma altura).
A gente já descobriu essas duas velocidades e a pressão em , então:
Mas a gente quer a diferença dessa pressão com a pressão atmosférica ( logo:
Passo 4
d)
Agora nós queremos achar o valor de . Essa é a opção mais difícil. Vamos esquecer um pouco de Bernoulli aqui e lembrar de stevin.
A coluna de líquido de altura está em equilíbrio. Isso quer dizer a soma da pressão do ponto E mais a pressão exercida pela coluna de líquido tem que ser igual à pressão atmosférica. Por quê? Bom, a pressão atmosférica empurra a coluna de fluido de baixo pra cima, assim como as outras duas pressões empurram de cima pra baixo. Elas precisam ser iguais pra que o sistema entre em equilíbrio, pois se não fossem, haveria uma força resultante e não haveria equilíbrio.
Vamos lá:
Só que como o sistema está em equilíbrio, a pressão em tem que ser a mesma que em . Perceba que os pontos estão ligados apenas por um cano com ar. Como o ar está parado, ele apenas comunica a pressão de um ponto ao outro. Logo:
Resposta
a)
b)
c)
d)