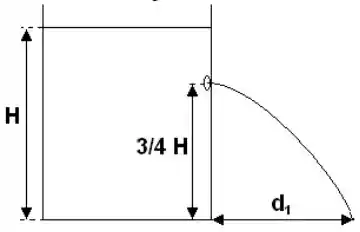
Considere um grande reservatório contendo um líquido de massa específica . Suponha que a altura do líquido seja e que é feito um furo pequeno no reservatório a da altura , conforme mostra a figura. Saindo pelo orifício, o líquido atinge uma distância da base do reservatório.
a) Calcule essa distância .
b) Calcule a altura de um segundo furo feito abaixo do primeiro e tal que o alcance do líquido saindo dele seja igual ao do primeiro. Para os seus cálculos, suponha que o nível do reservatório não se altera durante todo o processo.
Passo 1
a)
Vamos aplicar Bernoulli entre a superfície do fluido e o ponto onde há o fluido, usando o nível do chão como o nível zero de referência.
E essa é a velocidade com que o fluido sai pelo orifício. Agora vamos dar uma lembrada de Física 1( Caso não se lembre, acesse o nosso material de Física 1):
O tempo de queda de um corpo submetido a uma altura e sujeito à uma gravidade é:
Como
Então a distância será:
Passo 2
b)
Vamos chamar de a distância da superfície até o ponto que queremos achar. Logo, a altura que a gente procura vai ser . Aplicando Bernoulli entre o ponto do furo e a superfície:
O tempo de queda do fluido será:
Logo:
Comparando esse resultado com
Resolvendo essa equação, encontramos:
O caso corresponde ao caso do enunciado, pois ai a altura fica: . Então a gente deve usar :
Pronto (:.
Resposta
a)
b)