A figura abaixo mostra um jorro de água saindo por um furo a uma distância h da superfície de tanque cuja altura da água é H.
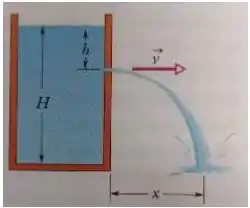
a) Calcule a que distância x que a água atinge o solo em termos de h e H.
b) A que profundidade deve ser feito um segundo furo para dar o mesmo valor de x?
c) Calcule a profundidade para a qual a distância que a água atinge o solo é máxima.
Passo 1
a) Aqui, temos uma questão de cinemática, onde o movimento horizontal é um movimento retilíneo uniforme com velocidade v, e o vertical é um movimento retilíneo uniformemente acelerado, com aceleração g.
Na horizontal,
Na vertical,
Jogando o tempo em ,
Passo 2
Só que a velocidade não é um dado do problema, apenas H e h.
Como podemos calcular a velocidade de saída então?
Se pensarmos numa linha de corrente que sai da superfície do líquido e vai até o furo, saindo com velocidade , podemos aplicar a equação de Bernoulli
Na superfície do líquido, a pressão é a atmosférica (), a velocidade é praticamente nula () e a altura em relação a altura do furo é . No furo, a pressão também é somente a atmosférica (), a altura em relação ao furo é () e a velocidade queremos descobrir (). Substituindo
(O valor mágico da hidrodinâmica)
Substituindo em x,
Passo 3
b) Para qual obtemos o mesmo valor de x?
Para resolver isso, presta atenção que a equação que temos para tem uma raiz quadrada. Se elevarmos ao quadrado, teremos uma equação do segundo grau. Equações do segundo grau tem duas raízes, uma que é o que já temos, e o outro é o segredo do sucesso. Vamos lá:
Queremos calcular para h,
Fazendo uma bhaskara aqui
São os dois valores possíveis para que tenhamos o mesmo valor de x.
Passo 4
c) Qual a profundidade (h) para o alcance () ser máximo?
Para ser máximo, a derivada tem que ser igual a zero,
Daí tiramos que o numerador tem que ser zero,
Resposta
a)
b)
c)