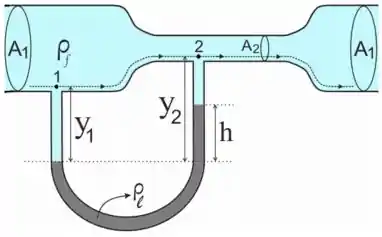
O medidor de Venturi é usado para se obter a velocidade de escoamento estacionário de um fluido não viscoso em uma tubulação. Considere um fluido incompressível, de densidade , que escoa em uma tubulação com área ade seção transversal Na região de estrangulamento, a área é reduzida pra , e um tubo manométrico é instalado como mostrado abaixo (vide figura). Suponha que o liquido do manômetro também seja incompressível e tenha densidade . NÃO despreze termos como
- Obtenha a diferença de pressão entre os pontos 1 e 2 em termos dos dados e da velocidade no ponto 1
- Determine a altura lida no medidor em função da diferença de pressão entre os pontos 1 e 2.
- Determine a velocidade de escoamento em termos dos dados do problema e das respostas anteriores.
Passo 1
a)
Aqui a gente vai ter que aplicar Bernoulli entre os pontos 1 e 2.
Quando a gente usa Bernoulli, a gente precisa definir um ponto de altura
O ponto que usamos já tá definido ali na figura, é o nível que saem as alturas e
Ok, então o resto é só aplicar os valores de pressão altura e velocidade:
Beleza? Só que a gente não sabe . Então precisamos usar a equação da continuidade, certo?
Então:
Pronto (:
Passo 2
b)
A gente vai usar o principio de Stevin pra resolver isso. No nível de altura , as pressões são iguais pois tem a mesma altura. Então a pressão do lado esquerdo é a mesma que do lado direito:
A pressão do lado esquerdo vale:
OU seja, é a soma da pressão 1 mais a pressão devido a coluna de líquido azul.
Preste atenção nisso, pois temos dois fluidos ali.
E a pressão do lado direito vale:
Ou seja, é a soma da pressão 2, mais a pressão causada pela coluna de fluido e a coluna de fluido de liquido
A altura da coluna de liquido é (veja na figura).
A altura da coluna de é
Passo 3
Vamos igualar as duas:
Passo 4
c)
Temos duas expressões pra e uma delas tem . Vamos igualar as duas:
Resposta
a)
b)
c)